The term “Lagrangian” in the realm of particle physics evokes a tapestry of theoretical constructs that underlie the dynamics of physical systems. It refers to a pivotal concept in the formulation of classical mechanics, particularly within the framework of analytical mechanics. This essay aims to unravel the intricate meaning of the term “Lagrangian,” illustrating its profound implications for understanding the behavior of particles and the fundamental interactions governing the universe.
At its core, the Lagrangian represents a function that encapsulates the dynamics of a physical system. Traditionally denoted as ( L ), the Lagrangian is defined as the difference between the kinetic energy (T) and the potential energy (V) of a system: ( L = T – V ). This formulation promises a significant shift in perspective, moving away from the Newtonian mechanics that prioritizes forces and accelerations. Instead, it invites one to engage with the energies involved in the motion, facilitating a more holistic understanding of the mechanisms at play.
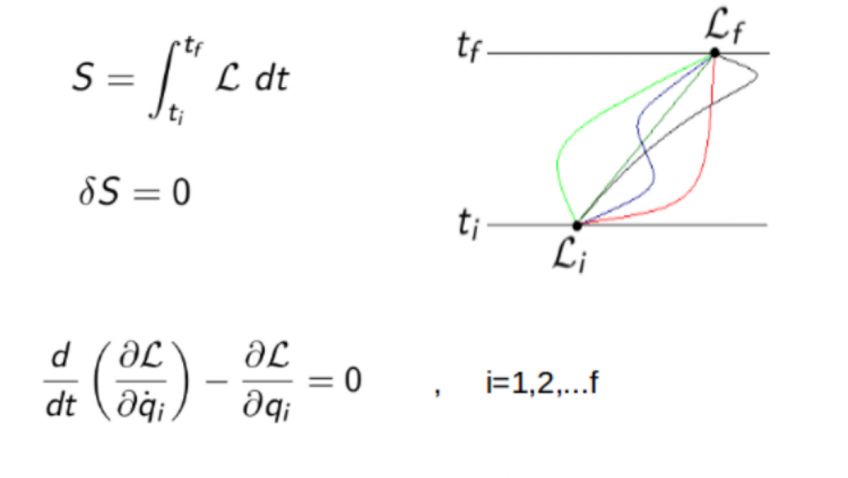
One of the most compelling features of the Lagrangian framework is its foundation in the principle of least action, also known as Hamilton’s principle. This principle posits that the actual path taken by a system between two states is the one that minimizes the action, a quantity defined as the integral of the Lagrangian over time. This notion fundamentally alters our perception of motion, suggesting that nature itself is guided by an underlying elegance that transcends mere physical forces.
The Lagrangian formalism extends its reach into various disciplines, offering insights that bridge classical mechanics, quantum mechanics, and field theory. Within particle physics, the Lagrangian serves as a central pillar for constructing quantum field theories. Here, it encapsulates the dynamics of particles and fields, encoding information about the interactions confined within a given system. This versatility nurtures curiosity, as it positions the Lagrangian not merely as a mathematical tool, but as a lens through which the symmetries and conservation laws of nature can be deciphered.
When examining the role of the Lagrangian in particle physics, it becomes essential to consider its implications in a relativistic context. The advent of special relativity necessitated the revision of classical concepts, culminating in the development of a relativistic Lagrangian. This formulation ensures consistency with Einstein’s theory, elegantly allowing for the incorporation of energy-momentum relations and guaranteeing that the speed of light remains invariant for all observers. Such adaptability underscores the Lagrangian’s capacity to unify disparate physical laws into a coherent framework.
Moreover, in the field of gauge theories, which underpin the Standard Model of particle physics, the Lagrangian plays an indispensable role. It encapsulates the symmetries of the electromagnetic, weak, and strong interactions, elucidating how particles acquire mass and interact through various force carriers. This intricate dance of particles and fields is articulated through the mathematical formalism of the Lagrangian, which retains a sense of beauty—exemplifying the interconnectedness of all things in the cosmos.
Central to the utility of the Lagrangian is its ability to derive equations of motion using the Euler-Lagrange equations. Through this method, one can succinctly derive the trajectories of particles by applying variational principles, a process that foregrounds the elegance of mathematical abstraction. This approach not only streamlines calculations but also unveils deep-seated relationships between seemingly disparate physical phenomena, thereby piquing the intellectual curiosity of those who pursue the nuances of theoretical physics.
The exploration of symmetries through the Lagrangian framework also leads to the profound realization that these symmetries are intimately connected to conservation laws via Noether’s theorem. For instance, the invariance of the Lagrangian under time translations corresponds to the conservation of energy, while spatial translations result in the conservation of momentum. This revelation promises to shift one’s perspective: the exploration of fundamental symmetries is not merely a mathematical pursuit but a gateway to understanding the very structure of reality.
Additionally, the Lagrangian approach has inspired various extensions and generalizations, including the development of effective field theories and advances in string theory. These domains push the boundaries of conventional particle physics, as they endeavor to tackle questions surrounding quantum gravity and the unification of forces. Concepts derived from the Lagrangian framework continue to shape contemporary theoretical research, encouraging physicists to venture into uncharted territories of knowledge.
In summary, the meaning of “Lagrangian” in particle physics transcends its conventional definition as a mere mathematical construct. It embodies a sophisticated perspective on the laws of motion, a gateway to understanding symmetries and conservation principles, and a fundamental tool for constructing the theoretical underpinnings of particle interactions. The Lagrangian invites physicists and scholars alike to embrace a narrative that weaves together motion, energy, and the fundamental workings of the universe. As curiosity beckons, the study of the Lagrangian inspires continued exploration, urging us to unravel the mysteries that lie at the heart of existence itself.