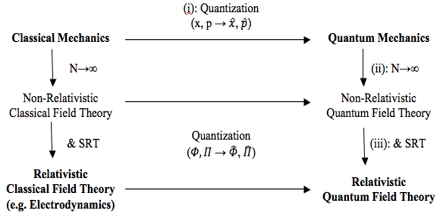
Quantum Field Theory (QFT) represents a foundational framework in modern theoretical physics that melds quantum mechanics with special relativity. It fundamentally re-conceptualizes the nature of particles and their interactions, providing a comprehensive language for describing the subatomic landscape. Through its mathematical rigor and conceptual clarity, QFT has revolutionized our understanding of the universe at its most elementary levels. This article delves into the intricacies of QFT, elucidating its nature, principles, and implications.
At its core, Quantum Field Theory posits that particles are not mere discrete entities but rather excitations or quanta of underlying fields that permeate all of space and time. This represents a paradigm shift from classical particle mechanics, where particles were viewed as point-like objects. In QFT, each fundamental particle—such as electrons, quarks, and photons—corresponds to a specific field. For instance, the electron is an excitation of the electron field, while photons are excitations of the electromagnetic field. This field-centric view facilitates the unification of various physical phenomena under a coherent theoretical umbrella.
The historical development of Quantum Field Theory emerged from the quest to reconcile the principles of quantum mechanics with the requirements of special relativity. In the early 20th century, physicists grappled with inconsistencies arising from quantum mechanics when applied to relativistic particles. The seminal works of figures like Dirac, who formulated the Dirac equation, laid the groundwork for a relativistic quantum mechanics that integrated these previously disparate domains. The introduction of QFT brought forth the notion of particle-antiparticle creation and annihilation, elucidating processes that occur in high-energy environments, such as those found in particle accelerators.
One of the most significant extensions of QFT is the development of gauge theories, which underpin our current understanding of the fundamental forces of nature. The Standard Model of particle physics, which is built upon the framework of QFT, describes three of the four fundamental interactions: electromagnetism, the weak nuclear force, and the strong nuclear force. Each of these interactions is mediated by gauge bosons, which can be understood as force-carrying particles associated with specific fields. For example, the photon mediates electromagnetic interactions, while gluons are responsible for binding quarks together in protons and neutrons.
A critical aspect of QFT is the methodology employed to calculate observable quantities. The perturbative approach, particularly the technique of Feynman diagrams, has become a hallmark of QFT calculations. Feynman diagrams visually represent particle interactions, enabling physicists to derive scattering amplitudes and cross-sections from complex integrals. This method significantly simplifies calculations, allowing for the systematic evaluation of processes such as particle collisions. However, not all interactions can be effectively treated through perturbative methods. Non-perturbative phenomena, such as confinement in quantum chromodynamics (QCD), require more sophisticated approaches to study.
The concept of renormalization is integral to addressing infinities that arise in QFT calculations. As one attempts to compute physical quantities associated with interacting fields, divergences frequently appear, necessitating a process to restore meaningful results. Renormalization involves redefining parameters, such as mass and charge, to absorb these infinities, leading to finite predictions for observable quantities. This counterintuitive procedure has profound implications, as it reveals the inherent connection between physical theories and the mathematical constructs that underpin them.
In addition to its successes, Quantum Field Theory is not without its challenges and limitations. While QFT has brilliantly explained a wide array of experimental results, its application to gravity remains elusive. Theories attempting to formulate a quantum version of general relativity have encountered substantial difficulties, yielding a fertile ground for ongoing research. String theory and loop quantum gravity are among various theoretical frameworks being explored in the quest for a unified theory that encompasses all fundamental forces, including gravity.
Moreover, quantum field theoretic ideas have permeated other domains of physics, yielding insights into condensed matter systems, cosmology, and statistical mechanics. In condensed matter physics, the concept of spontaneous symmetry breaking, akin to order parameters in phase transitions, has been elegantly described using field theoretical methods. In cosmology, QFT is employed to analyze the early universe, particularly in the context of inflation and the formation of cosmic structures.
In conclusion, Quantum Field Theory is a profound theoretical framework that reshapes our understanding of the universe at the most fundamental level. By portraying particles as excitations of fields and integrating relativistic principles, QFT elucidates the nature of fundamental forces and interactions. Despite its challenges, including the quest for a unified theory incorporating gravity, QFT has yielded remarkable insights across various fields of physics. As researchers continue to probe the depths of quantum fields and explore their implications, the journey through the quantum realm promises to unveil further layers of complexity and beauty in the fabric of reality.