As we traverse the enigmatic realm of quantum computing, one cannot help but ponder: how accurate are current quantum computers? This question not only invites a profound exploration of the technological advancements in the field but also presents an intellectual challenge that grapples with the inherent uncertainties and unique capabilities that characterize quantum systems. The journey into this realm elucidates the nuances of accuracy in quantum computations and the implications it holds for future innovations.
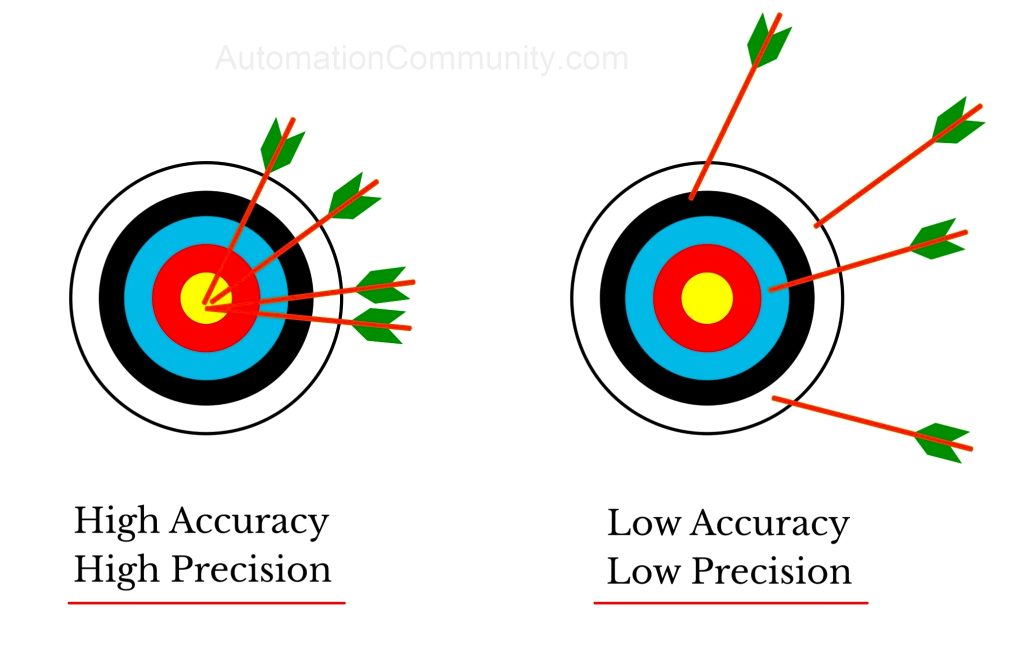
The notion of accuracy in quantum computing juxtaposes nicely against classical computing paradigms. In classical systems, accuracy is often a matter of binary fidelity—where results are either correct or incorrect. However, in the quantum domain, accuracy transcends mere correctness, encompassing aspects such as coherence, entanglement fidelity, and error rates. Understanding these parameters is crucial for a holistic grasp of the capabilities and limitations of current quantum technologies.
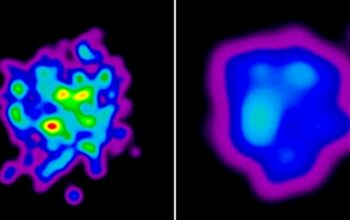
To appreciate the accuracy of quantum computers, one must first delve into the concept of qubits. Unlike classical bits, which are confined to the dichotomous states of 0 and 1, qubits leverage the principles of superposition and entanglement. This allows them to exist in multiple states simultaneously. However, this inherent complexity also leads to susceptibility to errors. Quantum decoherence, a phenomenon where qubits lose their quantum state due to environmental interaction, poses significant challenges. Consequently, accuracy in quantum computing is not merely about correct outputs but also ensuring that qubits remain stable and coherent throughout the computation process.
The fidelity of quantum gates— the fundamental operations performed on qubits— serves as a barometer for overall computational accuracy. Gate fidelity can be defined as the likelihood that a quantum operation accurately transforms a qubit from one state to another without inflicting errors. Current quantum computers, such as those developed by IBM, Google, and others, typically exhibit gate fidelities in the range of 90% to 99%. While this might seem commendable, it starkly contrasts with the precision found in classical computing systems, where operation fidelity nears 100%.
A pivotal challenge that arises from this disparity is error correction. Quantum error correction (QEC) is a burgeoning field aimed at mitigating errors that manifest during quantum computations. Traditional error correction techniques are inadequate due to the no-cloning theorem, which prohibits the replication of unknown quantum states. Instead, QEC employs intricate schemes involving logical qubits—essentially, qubits organized in such a way that they can collectively safeguard against errors. Techniques like Shor’s code and surface codes have emerged as solutions, yet they necessitate an exorbitant number of physical qubits to protect a single logical qubit, thus complicating the scalability of quantum systems.
The interplay between error rates and algorithmic accuracy yields interesting insights into the current state of quantum computing. For instance, during the execution of algorithms such as Shor’s algorithm or Grover’s algorithm, small inaccuracies can lead to profoundly different outcomes. Moreover, the exponential speed-up promised by quantum algorithms relies critically on the successful execution of these algorithms in the face of noise and errors. As a result, researchers are fervently exploring hybrid approaches that marry classical and quantum computing paradigms for tasks that are either computationally intensive or require more reliability.
Furthermore, one must consider the benchmarks against which quantum computers are measured. The quantum supremacy experiment conducted by Google illustrated the capability of a quantum processor to perform a calculation that would be practically impossible for even the most advanced classical supercomputers. Yet, the accuracy of the result and its practical applicability were points of contention among experts. This raises critical questions: Are we placing too high an expectation on current technology? And how do we navigate the dichotomy between groundbreaking achievements and their practical validation?
The discussion of accuracy in quantum computing also extends to the burgeoning field of quantum machine learning (QML). Here, the dual imperatives of harnessing quantum advantages while ensuring the fidelity of results become a salient concern. Algorithms designed for quantum variational classifiers or quantum support vector machines hold tremendous promise; however, the current accuracy of results remains a pivotal question. The sensitivity to initial states and the interface between classical data and quantum states contribute to the challenges of achieving reliable outputs.
As advancements continue to be made, the question of accuracy becomes an evolving narrative. Innovations incorporating advanced materials, novel qubit designs such as topological qubits, and the development of all-optical quantum processors promise to enhance coherence times and gate fidelities. Additionally, interdisciplinary approaches that bring together expertise from fields like condensed matter physics, computer science, and electrical engineering are instrumental in augmenting the reliability of quantum computations.
In conclusion, while current quantum computers exhibit impressive capabilities, the level of accuracy is impeded by contextual peculiarities distinctive to quantum mechanics. The ramifications of this accuracy—or lack thereof—extend across multiple domains, from cryptography to complex modeling in chemical reactions. As researchers navigate this intricate tapestry, the playful yet probing question remains: can we embrace a future where quantum accuracy transcends its limitations, transforming theoretical potential into practical reality? The path forward holds myriad possibilities, each beckoning exploration and discovery in equal measure.