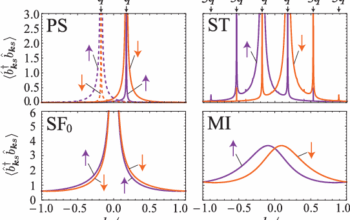
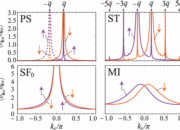
In the realm of quantum mechanics, Schrödinger’s equation stands as a pillar of theoretical understanding, delineating how quantum systems evolve over time. Its profound implications extend into various fields, most notably quantum computing. This computational paradigm leverages the principles of quantum mechanics to perform complex calculations at unprecedented speeds. Understanding how Schrödinger’s equation underpins quantum computing necessitates a thorough exploration of its fundamental principles, applications, and the unique challenges it presents.
Schrödinger’s equation can be classified into two primary forms: the time-dependent and time-independent equations. The time-dependent Schrödinger equation governs the behavior of quantum systems as they evolve, while the time-independent version is typically used for stationary states, often associated with bound systems. Both formulations are inherently mathematical, characterized by wave functions that encapsulate the probabilistic nature of quantum states. In quantum computing, these wave functions embody qubits, the essential unit of quantum information.
To comprehend the application of Schrödinger’s equation within quantum computing, it is essential to appreciate the concept of superposition. Qubits, unlike classical bits that assume definitive states of 0 or 1, can exist in a linear combination of these states. This feature is mathematically represented by the wave function derived from Schrödinger’s equation. The principle of superposition provides quantum computers their exceptional parallelism, allowing them to process a multitude of possibilities simultaneously. For instance, a quantum computer with just a few qubits can perform calculations corresponding to multiple classical bits, dramatically enhancing computational power.
The phenomenon of entanglement, another cornerstone in quantum mechanics, further illustrates the significance of Schrödinger’s equation in quantum computing. When qubits are entangled, the state of one qubit becomes intrinsically linked to the state of another, no matter the spatial separation between them. This relationship can also be elucidated through Schrödinger’s equation, which allows for the calculation of the combined wave function of entangled qubits. Entangled qubits empower quantum computers to execute complex operations that are infeasible for classical systems, enabling rapid problem-solving capabilities across various applications.
Specific algorithms in quantum computing are directly influenced by the principles elucidated through Schrödinger’s equation. A prime example is Shor’s algorithm, which facilitates the factorization of large integers, a task that remains computationally intractable for classical systems. The algorithm exploits the quantum properties of superposition and entanglement, as described by Schrödinger’s dynamics, to achieve exponential speedups. Similarly, Grover’s algorithm showcases the dramatic acceleration of search capabilities within unstructured databases, demonstrating the practical utilities derived from quantum mechanics.
Quantum gates also play a pivotal role in manipulating qubit states within quantum circuits. These gates, analogous to classical logic gates, perform operations on qubits and are faithfully described by unitary transformations—mathematical operations that preserve the norms of the wave function. The application of these transformations is inherently rooted in the framework set forth by Schrödinger’s equation, ensuring that the resultant state of a qubit remains valid within the probabilistic realm of quantum mechanics. Techniques for constructing and coherently integrating such gates form a fundamental aspect of quantum algorithm designs.
Despite its immense potential, the implementation of quantum computing is fraught with challenges. Quantum decoherence poses a significant threat to the integrity of quantum states, disrupting the delicate balance needed for superposition and entanglement. Decoherence arises when qubits interact with their environment, leading to the collapse of their wave functions, as characterized by Schrödinger’s equation. A thorough understanding of these dynamics is essential for developing robust quantum error correction techniques, enabling the mitigation of decoherence’s adverse effects and the reliable execution of quantum algorithms.
Moreover, the physical realization of qubits—whether through superconducting circuits, trapped ions, or topological qubits—necessitates considerations of system design that minimize decoherence while maximizing information fidelity. Engineering solutions must adhere to the underlying quantum principles established by Schrödinger’s equation, thus aligning the physical realizations with theoretical expectations.
As quantum computing transitions from theoretical exploration to practical application, researchers continue to dissect the implications of Schrödinger’s equation across varying contexts. Its role in elucidating quantum phenomena drives an ongoing dialogue regarding the potential of quantum computers in fields as diverse as cryptography, optimization, and simulation of quantum systems themselves.
The integration of Schrödinger’s equation into quantum computing embodies a harmonious relationship between rigorous mathematical theory and cutting-edge technological advancement. This intersection not only illuminates the foundational mechanics of quantum systems but also heralds a new era of computation where complexity is tamed through quantum principles. As the field progresses, the dynamism of Schrödinger’s equation will undoubtedly cultivate further revelations, cementing its status as a foundational construct in both physics and computer science. In summary, the usage of Schrödinger’s equation in quantum computing is multifaceted, serving as a bridge between theoretical inquiries and computational realities, shaping the future of technology in profound ways.