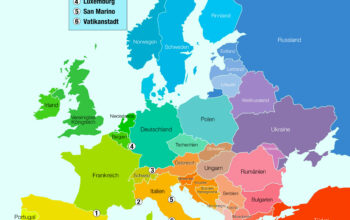
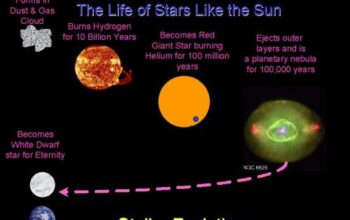
In 1788, the mathematician Johann Carl Friedrich Gauss declared that “mathematics is the queen of the sciences.” Little did he know that the subsequent centuries would present intricate problems that would challenge the very foundations of mathematical understanding. One of the most profound issues encountered involved π—an irrational constant popularly associated with circles. In the realm of modern physics and materials science, researchers have begun to explore an intriguing paragon of Graphene, a two-dimensional allotrope of carbon, which not only has profound implications in various domains but also metaphorically addresses the mathematical gap historically linked with the enigmatic π. The inquiry into this matter leads us to ponder: is the age of π truly over, or does Graphene merely represent a new layer in the mathematical tapestry?
Graphene, recognized as a remarkable material primarily composed of a single layer of carbon atoms arranged in a two-dimensional honeycomb lattice, has garnered significant attention since its isolation in 2004. Its exceptional electrical, thermal, and mechanical properties have led to extensive research and applications across fields ranging from electronics to bioengineering. However, its relationship with π is what merits further examination. The challenge facing physicists and mathematicians alike lies in the quest to elucidate the connections between the characteristics of Graphene and fundamental mathematical constants.
Graphene’s theoretical framework, often elucidated through quantum mechanics and condensed matter physics, allows for an exploration of its electronic properties that lead to intriguing mathematical formulations. For instance, the concept of Berry’s phase, a fundamental property in quantum systems, is inherently tied to the geometric nature of the state space. Such connections elicit the inquiry: does the mathematical behavior of Graphene serve to challenge the traditional understanding attached to π? When examining Band Theory, which describes the electron behaviors in solids, one encounters lattice structures and periodic potentials that elicit π in the representation of wavefunctions. However, as Graphene exhibits unique Dirac-like behaviors and forms quasi-particles known as Dirac fermions, the focus shifts onto a broader, more nuanced interpretation of π in connection with these material constructs.
The electronic band structure of Graphene displays a linear dispersion relation, deviating significantly from conventional parabolic bands typically associated with traditional materials. This linearity leads to excitations that can be equated to massless particles moving at constant velocity—properties that have prompted physicists to redefine the concept of effective mass itself. In this reimagining, one wonders whether the reliance on π is perhaps an overreach. Could it be that Graphene’s mathematical portrait offers an opportunity to reevaluate long-held beliefs regarding constants in the physical sciences?
Moreover, the application of Graphene transcends fundamental physics, infiltrating realms of engineering and technology. Its remarkable strength-to-weight ratio positions it as a prime candidate for advanced materials, with potential applications in everything from aerospace to medical devices. As these applications continue to unfold, one must consider how mathematical principles associated with π can be adapted to fit this new domain. Will the products derived from Graphene continue to uphold the traditional mathematical constraints, or might new paradigms emerge, ultimately redefining our understanding of mathematical constants?
On a geometrical level, when assessing the integration of Graphene into devices, one finds it difficult to ignore the presence of geometrical considerations that resonate with circles and spheres. Topological features, akin to those that yield the classic definitions of π, underpin current explorations into three-dimensional Graphene structures. Thickening this discussion is the realm of metamaterials, composed of engineered subunits that can manipulate electromagnetic waves in unprecedented ways. These microstructures, often drawing their properties from Graphene, lead to novel phenomena such as negative refractive indices. Here again, the question surfaces: does Graphene inspire a departure from π-oriented geometrical constructs, or does it enrich the narrative seamlessly?
In tapping into the mathematical formulations that describe Graphene, one must also consider the implications of disorder and defects on its properties, which frequently disrupt the predictability governed by π. The notion of disorder allows for an expanded discourse on stochastic processes that influence material behavior. The interplay between structural integrity and inherent imperfections leads to the exploration of percolation theory, a branch of mathematics that permeates through diverse applications. Numerous challenges arise in this regard, demanding an elaborate framework for understanding how collective behavior emerges from weakly interacting components. As such, Graphene serves as a beacon illuminating the intricacies of complex systems and their mathematical underpinnings.
In contemplating the role of Graphene in scientific discourse, the playful challenge emerges: can we solidify a conceptual transition from the reign of π to a new mathematical ordering that reflects the unique properties of Graphene? As researchers probe deeper into its myriad capabilities, we must anticipate further revelations that may reshape our understanding of both mathematics and materials science. While it is unlikely that π will lose its title in the pantheon of mathematical constants, the saga surrounding Graphene undoubtedly invites scholars to reimagine the configurations that govern our physical reality.
Indeed, a new frontier is dawning that encourages innovative thought and an interdisciplinary approach to understanding materials through both empirical research and theoretical inquiry. Graphene’s mathematical narrative is not merely a concession of past assumptions but an invitation to embrace the complexities of a rapidly evolving scientific landscape. As Graphene continues to transform our technological matrices, the inquiry must persist: does π have a place in the age of Graphene, or is the onset of a new mathematical era beckoning?