The Kondo problem represents a deeply intricate phenomenological puzzle within the realm of condensed matter physics. It emerges from the interaction of localized magnetic moments, typically associated with impurity atoms, with the surrounding conduction electrons in a metallic host. This deceptively simple premise unveils a plethora of underlying complexities and catalyzes a rich tapestry of physical phenomena, illustrating why it has garnered significant attention from physicists over the decades.
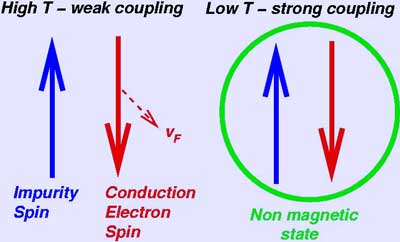
At its core, the Kondo effect embodies a counterintuitive behavior: as temperature diminishes, the resistivity of certain metals containing magnetic impurities actually increases. This is in stark contradiction to classical expectations, which typically assert that resistivity should decrease with lowering temperature due to reduced electron scattering. The Kondo effect shines in its ability to modify the envisioned behavior of metals through electron hybridization with localized spins, thus laying the groundwork for discussions surrounding quantum fluctuations and many-body physics.
One of the most intriguing aspects of the Kondo problem is its renormalization group (RG) behavior, which reveals critical insights into the nature of the coupling between impurities and conduction electrons. Under these conditions, a weak coupling between the impurity spins and the conduction electrons gets progressively enhanced as the energy scale diminishes, leading to a highly nontrivial low-temperature behavior characterized by a logarithmic increase in resistivity. This subtle yet profound effect is a hallmark of quantum many-body systems, wherein collective phenomena arise from interactions among vast numbers of particles.
The Kondo model employs an effective Hamiltonian that encapsulates this interaction. Initially proposed by Jun Kondo in 1964, the model simplifies the problem by focusing on a single localized spin interacting with a sea of conduction electrons. Mathematically, the model is described by a Hamiltonian featuring terms that represent the kinetic energy of the electrons and an interaction term detailing the coupling to the localized spin. The absence of a simple analytic solution to this model emphasizes the necessity of advanced computational methods, such as numerical renormalization group (NRG) techniques, which have emerged as formidable tools for tackling the complexities of the Kondo problem.
Furthermore, the Kondo effect offers a diverse spectrum of manifestations based on the nature of the impurity. When considering magnetic impurities, the spin-½ Kondo model is often employed, while situations involving higher spin impurities may lead to the investigation of multi-channel Kondo effects. Each variant presents its own set of challenges and predictions, enhancing the richness of the Kondo problem. For instance, the multi-channel Kondo problem describes situations where multiple conduction channels interact with the impurity, resulting in a nontrivial ground state that is entangled and exhibits exotic behavior, including the emergence of fractionalized excitations and non-Fermi liquid properties.
Beyond resistivity, the Kondo effect plays a pivotal role in influencing several other physical properties. Specific heat, susceptibility, and spin dynamics exemplify critical areas of investigation. As temperature approaches absolute zero, the specific heat associated with the Kondo interaction showcases an anomalous linear temperature dependence, a signature characteristic of conformally invariant ground states. Such behavior indicates the profound intricacies of low-energy excitations within correlated electron systems, ultimately providing a conduit for deeper exploration into the quantum critical phenomena that permeate systems beyond mere metallic conductors.
Moreover, the Kondo problem serves as a crucial principle in the study of quantum dots, which are nanoscale semiconductor devices that confine electron motion in all three spatial dimensions. In these confined systems, the interplay between localized quantum states and the continuum of electron states generates phenomena akin to those observed in bulk materials, thus demonstrating the Kondo effect on a miniaturized scale. The ability to manipulate quantum dots and examine their Kondo-regime has opened avenues for understanding coherence, entanglement, and the pursuit of quantum computing technologies.
Another noteworthy dimension of the Kondo problem is its relation to topological insulators and emergent phenomena within those materials. Topological states of matter present intriguing parallels to the Kondo effect, enriching continued discourse surrounding many-body localization, quantum entanglement, and emergent quantum criticality. The permeability of the Kondo problem towards hybridizing with this broader landscape underscores its fundamental role in contemporary condensed matter research.
The fascination with the Kondo problem lies not only in its important theoretical implications but also in its pervasive applications across varied domains of physics. The manner in which the Kondo effect challenges conventional wisdom about electron scattering and conductivity has engendered a paradigm shift in our understanding of correlated electron systems. It serves as a vital component for both fundamental research and practical applications, encompassing fields from materials science to quantum information technology. The Kondo effect continues to stimulate inquiries regarding the nature of quantum entanglement and the interplay of disorder in quantum systems, ensuring its status as a captivating topic in condensed matter physics.
In conclusion, the Kondo problem epitomizes the profound complexities rooted within condensed matter physics, transforming mundane metal behavior into a fascinating clinical study of quantum interactions. Through the lens of the Kondo effect, physicists unravel the enigmatic tapestry of electron spin interactions, endless behavior of resistivity, and the odyssey of many-body correlations. Investigating the Kondo problem offers an illuminating glimpse into the intricacies of the quantum world, revealing the essential significance of localized moments in a conductance-rich environment and aggravating the intellectual curiosity that drives the exploration of modern physics.