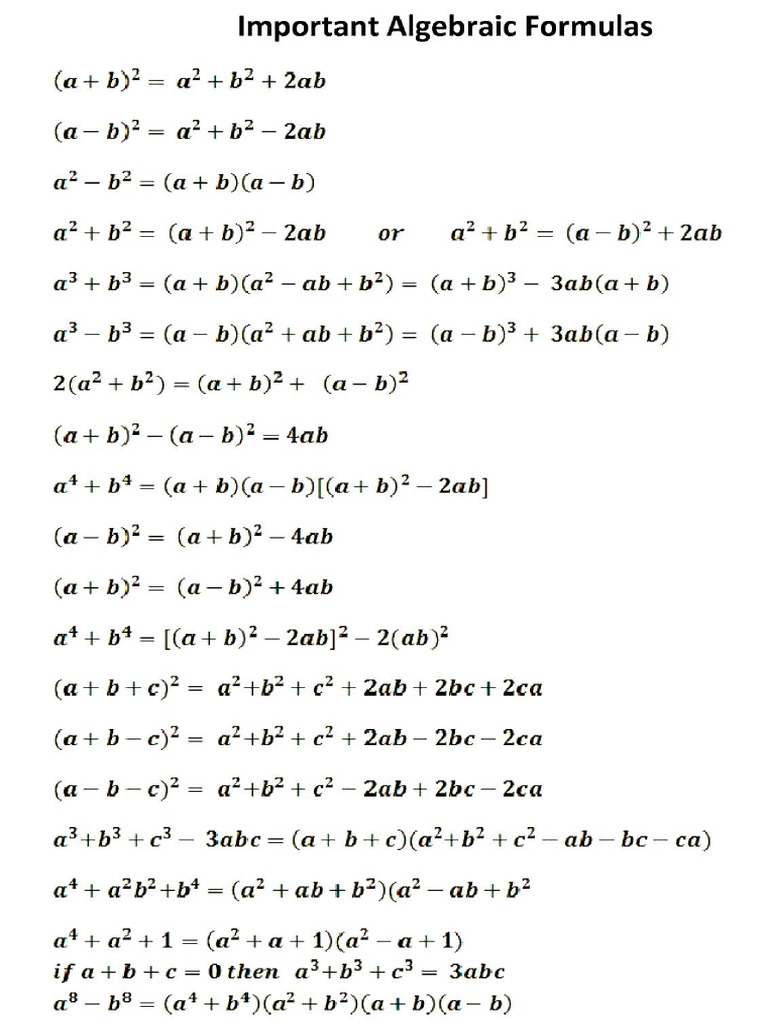Mathematics is often perceived as an enigmatic tapestry woven from abstract concepts and intricate relationships. Yet, at the core of this discipline lie self-made formulas—unique constructs that enable individuals to grapple with complex problems. These formulas transcend traditional methodologies, inviting scholars and enthusiasts alike to reconsider their approach to mathematical challenges. This discussion delves into the nature of self-made formulas, highlighting their utility and adaptability across various domains of mathematics.
The essence of a self-made formula is its personalized creation, born from an individual’s understanding and insights into specific mathematical problems. Unlike standard formulas, which are universally recognized and implemented, self-made formulas offer an opportunity for contextualization. This contextualization is critical, as it allows for more profound engagement with underlying principles, fostering deeper cognitive connections.
To embark on the journey of creating one’s own formulas, it is imperative first to appreciate the foundational principles of mathematics. This involves a meticulous examination of existing theories and theorems. By dissecting established formulas, one can identify the core components that can be manipulated or reimagined. For instance, consider the quadratic formula, which serves as a fundamental tool for solving second-degree polynomial equations. By exploring variations of this formula—instead of adhering strictly to its conventional application—one may conceive alternative expressions that yield equivalent results in unique contexts.
Diving into algebraic constructs, let us explore the transformation of known identities into personalized formulations. For example, while the Pythagorean theorem is universally accepted in Euclidean geometry, an innovator in the field might derive a customized formula based on unique geometric interpretations. By incorporating variables that represent specific conditions or constraints, one can craft a formula accommodating scenarios not immediately addressed by classical norms.
Additionally, the realm of calculus presents fertile ground for self-derived formulas. The principle of differentiation, with its roots in rates of change, allows for a plethora of personalized applications. A self-made formula might emerge from contextualizing a function within a real-world application, such as optimizing a manufacturing process. By recognizing the need to derive specific derivatives pertinent to that scenario, one can invent a formula that captures the essence of the problem accurately and efficiently. This creative act not only serves pragmatic purposes but also exemplifies the symbiotic relationship between theory and application.
Moreover, self-made formulas can extend into the realm of statistics, where understanding data requires a nuanced approach. The creation of custom statistical measures can be particularly illuminating. For example, one might deduce a unique formula for calculating averages that factor in outlier effects more effectively than standard deviations do. This formula could integrate additional parameters, such as weighted averages, offering a richer narrative of the data at hand. In this context, the formula not only serves a mathematical purpose but acts as a lens through which one can view the data from a more informed perspective.
The experimentation involved in formulating these equations fosters a culture of inquiry. When students or scholars allow themselves to deviate from established roads and venture into uncharted territories of mathematical thought, they cultivate an environment ripe for innovation. Encouraging this playfulness with numbers can ignite a passion for mathematics often hampered by the rigid structures of traditional education. The act of creating personal formulas becomes a journey of discovery, revealing not only the mathematics hidden in the world but also the potential for creative problem-solving inherent in all individuals.
Collaboration further enriches the process of developing self-made formulas. Engaging in dialogues with peers, experimenting through joint ventures, or exchanging ideas in academic settings can unveil new perspectives. One individual’s approach to formulating a mathematical problem may stimulate another’s ingenuity, opening pathways to diverse solutions. This collaborative environment acts as a crucible for creativity, facilitating the birth of formulas that are not just self-made but co-created in a collective pursuit of knowledge. Such synergy echoes the interconnected nature of mathematical exploration, emphasizing that innovation often thrives in community.
While the technique of constructing self-made formulas is empowering, it is essential to acknowledge the comprehensive nature of validation. A newly concocted formula should be rigorously tested and evaluated against known problems to ascertain its efficacy. This pivotal step ensures that personal insights translate into reliable solutions that adhere to mathematical rigor. Consequently, developing a personal formula becomes more than just an academic exercise; it transforms into a vital investigative journey that enriches one’s understanding of mathematics as a whole.
Lastly, it is crucial to view self-made formulas as an invitation to rethink the nature of problem-solving. They exemplify a shift from passive receptivity of established formulas to an active engagement through creation and innovation. The capacity to formulate equations that encapsulate personal insights fosters a sense of ownership over the learning process, instilling confidence and curiosity. Embracing this paradigm can radically alter the manner in which one interacts with mathematics, propelling individuals towards deeper comprehension and inventive applications.
In conclusion, the world of mathematics is not merely a collection of established rules but a fertile landscape for personal exploration. Self-made formulas are a testament to the creative potential residing within each individual, beckoning mathematicians to venture beyond convention and into the realm of innovation. By fostering a mindset that values personal engagement and creative problem-solving, practitioners can not only navigate complex mathematical terrains but also enrich the discipline with novel perspectives that challenge and refine our understanding of mathematics itself.