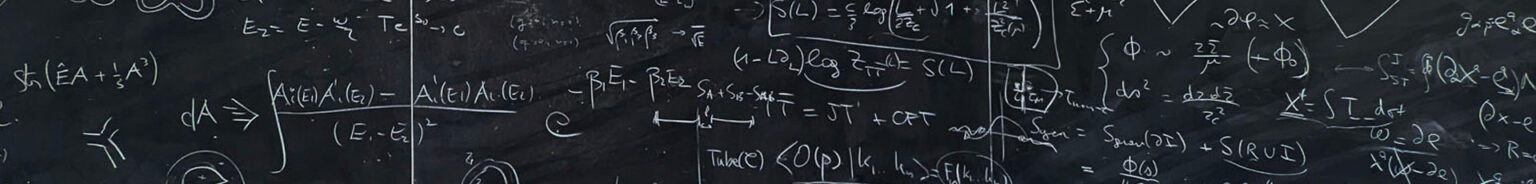The field of chaos theory, originating from complex dynamical systems in mathematics and physics, has evoked a fervent curiosity in scientists and mathematicians alike. Its central tenet revolves around the sensitive dependence on initial conditions, famously encapsulated in the metaphor of the butterfly effect, where small perturbations can lead to dramatically divergent outcomes. This intriguing juxtaposition between predictability and unpredictability underpins chaos theory, a domain replete with rich implications across various disciplines, including fluid dynamics, meteorology, and even economics. The Dirac Medal, an emblem of excellence in theoretical physics, shines a spotlight on the groundbreaking contributions to the understanding and modeling of chaotic systems. But can we truly tame the turbulent, or is the allure of chaos an inherent component of our universe?
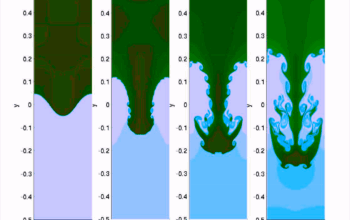
The question posed here serves as both a playful inquiry and a profound challenge. Similar to how the famous physicist Paul Dirac grappled with the paradoxes of quantum mechanics, contemporary researchers are now faced with the complexities inherent in chaotic systems. The pursuit of a comprehensive framework that could potentially predict outcomes in chaotic regimes tests the limits of mathematical models and computational techniques. For instance, the study of turbulence in fluids exemplifies this dichotomy. It is a well-observed phenomenon characterized by chaotic changes in pressure and flow velocity, findings from which have useful applications in engineering, meteorology, and even astrophysics. The exploration of this turbulent behavior raises the question: can we truly predict the behavior of a turbulent system, or are we merely engaging in a Sisyphean endeavor?
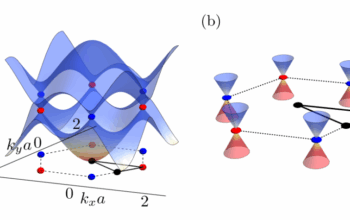
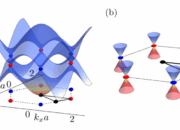
To appreciate the labyrinthine nature of chaos theory, one must first consider the mathematical foundations that underpin it. At its core lies the concept of dynamical systems, where the evolution of a particular system is described by differential equations. Many traditional systems exhibit equilibrium and regularity; however, the introduction of nonlinearity often leads to a cascade of complexities resulting in chaotic dynamics. Nonlinear systems are fascinatingly sensitive to initial conditions, and determining precise trajectories becomes increasingly challenging. This inherent unpredictability invites a re-evaluation of the methods employed to study these systems. Standard approaches may falter, leading researchers to explore innovative techniques, such as Lyapunov exponents, bifurcation diagrams, and fractal dimensions for characterizing chaos.
The implications of chaos theory extend beyond mere academic exercises; they resonate profoundly in various real-world applications. Weather forecasting, for instance, is a tangible demonstration of chaos theory in practice. Meteorologists rely on complex models to predict atmospheric conditions, yet the chaotic nature of weather systems means that forecasts become increasingly unreliable as they extend into the future. This paradox highlights the limitations of our understanding of chaotic systems and poses an intriguing question: is it possible to develop a ‘chaos-proof’ forecasting method? While the pursuit for precise long-term predictions remains elusive, the incorporation of chaos theory into predictive models can lead to more robust statistical interpretations of data.
Another field where chaos theory has made significant inroads is in the realm of neuroscience. The human brain, with its intricate neural networks, exhibits chaotic dynamics that correlate with cognitive functions and pathologies. Researchers are investigating how chaos theory can illuminate brain behavior, thereby enhancing our understanding of cognition and neural disorders. The interplay between chaos and order within the brain fosters a dynamic equilibrium that may contribute to cognitive flexibility. Yet, this prompts a provocative reflection: if chaos is instrumental to optimal brain function, should we reconsider the paradigmatic emphasis on stability in cognitive science?
In the realm of theoretical physics, the insights garnered from chaos theory extend to fundamental questions about the universe itself. Consider the behavior of particles in quantum field theories. The nonlinearity in certain quantum systems invites a potential framework that connects quantum chaos with classical chaos. The Dirac Medal recognizes those who have transcended conventional boundaries in physics by exploring these intersections. As research advances, scholars ponder whether a unified understanding of both chaotic and quantum systems could illuminate the very fabric of reality.
Moreover, the challenges presented by chaos theory catalyze discussions that reach into philosophy and epistemology. The debate regarding determinism versus indeterminism is rekindled in light of chaos theory, as it raises substantial inquiries about the nature of science itself. If chaos renders long-term predictions futile, how do we reconcile this with our pursuit of objective truth? Can scientific inquiry, then, be seen as an endeavor of approximations rather than absolutes? Situating chaos theory within these philosophical discourses encourages a more nuanced understanding of what it means to ‘know’ in the scientific context.
As we delve deeper into the mysteries of chaotic systems, the quest to tame the turbulent remains as captivating as ever. While researchers wield advanced mathematical models and computational simulations to navigate the treacherous waters of chaos, the path ahead is fraught with uncertainty and exhilaration. The inquiries posed by chaos theory—its implications for predictability, its applications across various fields, and its philosophical reverberations—invite an expansive contemplation of the nature of our universe. Ultimately, perhaps the charm of chaos lies not in subduing its tumult but in embracing the enigmatic beauty that complexity brings.
In summary, the Dirac Medal, symbolizing the pinnacle of achievement in theoretical physics, acknowledges the audacity of thinkers striving to unravel the perplexing world of chaotic phenomena. The explorations inspired by chaos theory continue to challenge the assumptions of conventional knowledge and beckon the scientific community toward a frontier rich with questions yet to be answered.