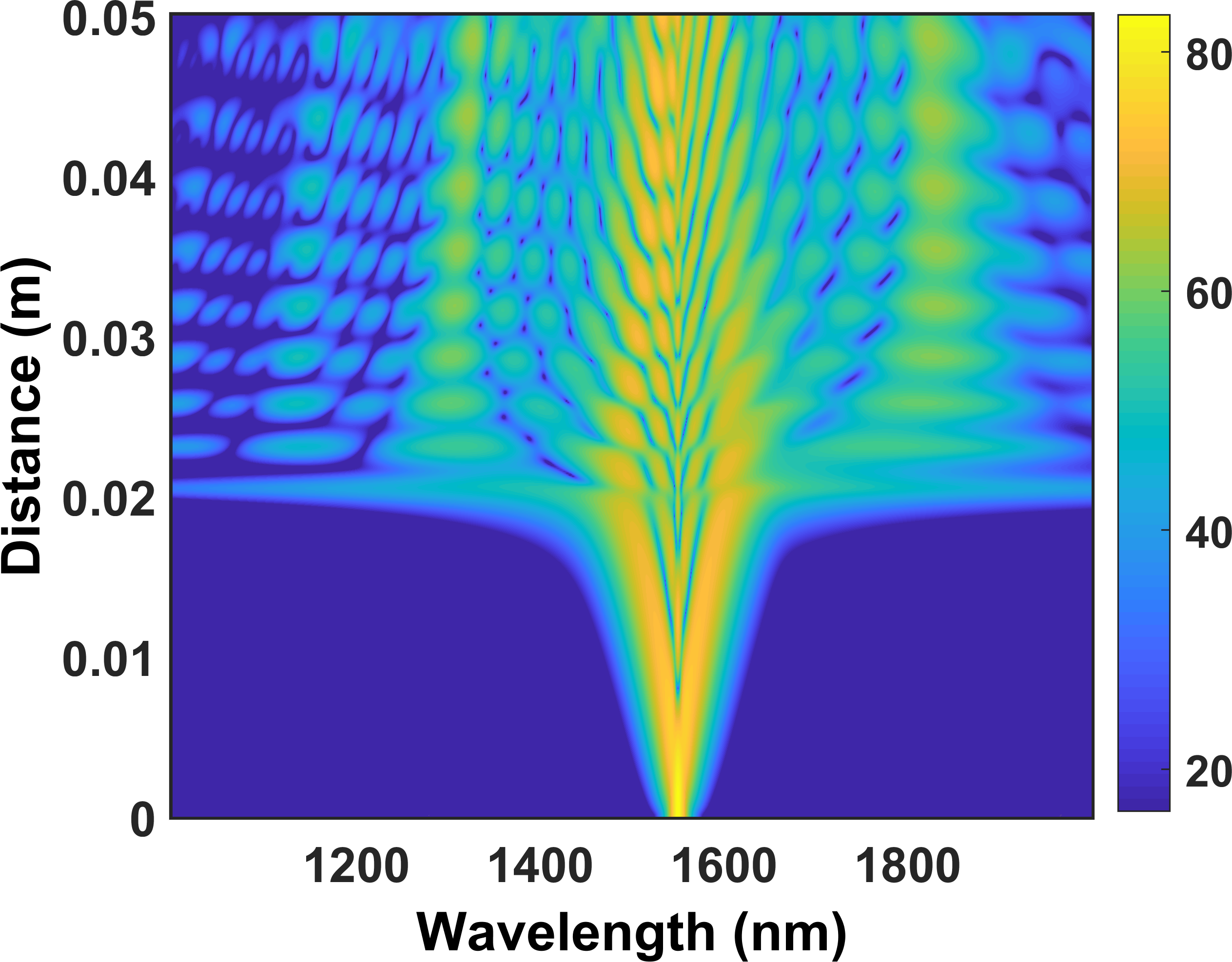
Nonlinear optics is a fascinating and complex field that delves into the interaction of light with matter under conditions where the linear approximation no longer suffices. In the realm of physics and optical engineering, this discipline is pivotal for the development of advanced technologies and a more profound understanding of fundamental phenomena. However, the question remains: how difficult is nonlinear optics? This inquiry warrants thorough exploration across various dimensions, including foundational concepts, mathematical complexities, experimental challenges, and applications that underscore the richness of the field.
To commence, the foundation of nonlinear optics is built upon the principles of classical electromagnetism and quantum mechanics. In linear optics, the response of a medium to an electromagnetic field is directly proportional to the amplitude of the light. This linearity permits straightforward modeling and analysis. In contrast, nonlinear optics emerges when the optical intensity exceeds a threshold where the medium’s refractive index becomes dependent on the light intensity itself. This phenomenon leads to various effects such as self-focusing, harmonic generation, and the Kerr effect. Understanding these fundamental dynamics requires a firm grasp of not only standard optical principles but also a broad comprehension of vector fields and wave propagation theory.
Mathematical intricacies become apparent when one begins to navigate the theoretical framework of nonlinear optics. The governing equations often extend beyond Maxwell’s equations, incorporating nonlinear terms that complicate solutions. The nonlinear Schrödinger equation, for instance, plays a central role in describing wave packet dynamics within nonlinear media. Solutions to such equations can be challenging to derive and often necessitate advanced mathematical techniques, including asymptotic analysis and numerical methods. Therefore, one must contend with a steep learning curve when transitioning from linear to nonlinear frameworks.
A pivotal aspect of nonlinear optics is the array of phenomena it encompasses. Each effect presents unique challenges and intricacies. For example, frequency doubling, or second-harmonic generation (SHG), requires precise phase matching conditions to achieve a coherent interaction. This necessitates not only a thorough comprehension of the crystal optics but also an adeptness at manipulating experimental parameters such as temperature and orientation. Similarly, self-phase modulation and four-wave mixing invoke intricate interactions that necessitate sophisticated experimental setups and real-time diagnostics to observe and characterize.
The experimental component of nonlinear optics further amplifies the difficulties associated with this discipline. Setting up experiments often involves dealing with high-intensity laser systems, which present risks and technical hurdles. The construction of stable optical setups can be logistically demanding, requiring meticulous alignment, control of environmental factors, and the integration of high-grade materials with precise optical properties. Moreover, the acquisition and interpretation of data from nonlinear optical experiments often require advanced techniques such as time-resolved spectroscopy or frequency-resolved optical gating, each of which carries its own set of complexities.
In addition to the technical and theoretical challenges, the field is continuously evolving, with ongoing research opening new avenues and concepts that expand the scope of nonlinear optics. Recent advancements such as topological photonics and quantum nonlinear optics are precipitating a re-evaluation of conventional wisdom and sparking debates regarding the interpretation of complex interactions. This dynamic nature of research makes it imperative for scholars in the field to stay abreast of the latest developments, oscillating between fundamental and applied knowledge.
Furthermore, the practical applications of nonlinear optics amplify its prominence in both academic research and industrial settings. From optical communication systems that leverage phenomena such as soliton propagation to medical imaging technologies exploiting nonlinear contrast agents, the implications are substantial. Technologies such as laser sources used in material processing, frequency combs in metrology, and optical parametric oscillators showcase nonlinear optics’ contributions to advancement in multiple disciplines.
Additionally, in the realm of emerging technologies, nonlinear optics continues to be at the forefront of innovation. Applications in quantum information science are particularly noteworthy, where the control of photon-pair generation through nonlinear processes enhances capabilities for secure communication and computational tasks beyond classical limits. Such potential breakthroughs underscore the relevancy and excitement surrounding the field, despite the inherent complexities involved.
In conclusion, while nonlinear optics poses a plethora of challenges, from its demanding mathematical formulations and theoretical constructs to its experimental intricacies and evolving applications, it is simultaneously a rich and rewarding area of study. The capacity to harness and manipulate light at nonlinear thresholds underscores not only the sophistication of physical principles at play but also the profound potential for impacting technology and science. Prospective scholars should be prepared to engage deeply with both the theory and practice of nonlinear optics, nurturing a resilience and curiosity that will ultimately serve them well in navigating this intricate landscape.