In the realm of quantum mechanics, the notion of qubits heralds a transformative leap from classical computation paradigms to quantum computation. But how would one undertake a simple calculation using these enigmatic entities? This inquiry leads us to the very essence of quantum information processing, which operates under fundamentally different principles than those governing classical bits.
To commence this exploration, let us ponder a playful question: What if you had the opportunity to not merely represent a single binary value—such as a 0 or a 1—but to encompass an infinitude of possibilities all at once? This is the extraordinary promise offered by qubits. Each qubit, through the phenomena of superposition, can inhabit a state that is a weighted combination of both 0 and 1, thereby extracting nuanced computational power.
For our illustrative example, consider the task of calculating the function (f(x) = x^2 ) for small integers, where ( x ) can take on the values {0, 1, 2, 3}. How would we approach this computation utilizing qubits? This endeavor necessitates grasping the foundational constructs of quantum mechanics and quantum algorithms.
First, initializing our qubits is paramount. The simplest form of encoding the inputs into qubits involves representing the integers with binary states. For example, 0 can be represented as |00⟩, 1 as |01⟩, 2 as |10⟩, and 3 as |11⟩. In a quantum state notation, our system may adopt a series of qubits corresponding to these representations. If one utilized two qubits, the representation would enable encoding up to four distinct values, which aligns perfectly with our integer set.
The procedure begins with a meticulous initialization step. Initiating the qubit states would entail applying a sequence of quantum gates that manipulate the qubit states suitably. In quantum computing, a ‘gate’ functions similarly to a classical logic gate, but it facilitates operations that can generate interference patterns through superposition and entanglement.
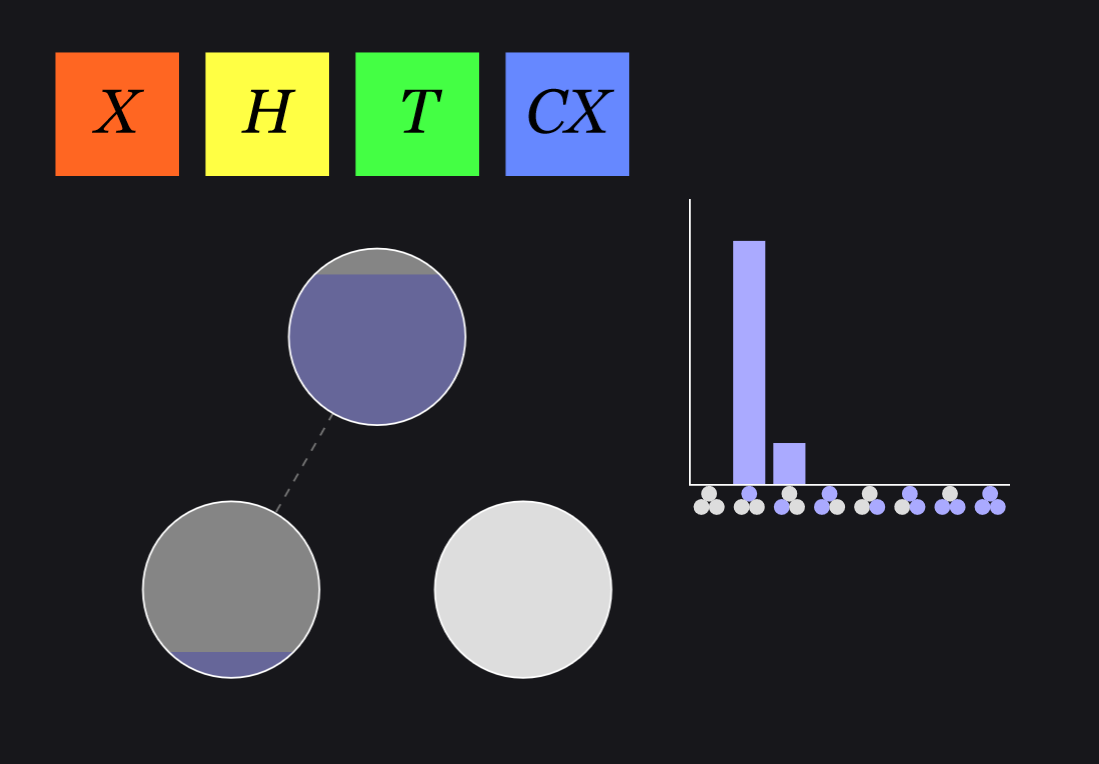
One might invoke the Hadamard gate at the outset to place each qubit into a superposition state. The Hadamard gate effectively transforms the qubit state from a computational basis into an equal superposition. For instance, applying a Hadamard gate on a qubit initialized to |0⟩ would yield the state |+⟩, defined as (frac{1}{sqrt{2}} (|0⟩ + |1⟩)).
Following the initialization phase, the quantum algorithm must be designed to compute our designated function (f). Herein lies an intriguing challenge: conventional arithmetic operations necessitate components such as addition and multiplication, which do not translate directly into the quantum framework. The quantum Fourier transform, a pivotal component of many quantum algorithms, could be beneficial for more complex functions, but here we can simplify our approach.
To compute (f(x)), we can invoke a sequential algorithm that integrates iterated qubit manipulations. A quantum circuit can be constructed, wherein each step corresponds to the calculation of (x^2). The quantum gates employed can include CNOT gates for conditional operations, which allow us to encode the output directly into predetermined qubit states.
For instance, as the algorithm iterates through possible inputs, the qubits corresponding to each input value can be multiplied using quantum operations. Therein, a (to borrow classical terminology) ‘recursive’ approach may be employed: we start from the qubit representing 0 and create transitions reflecting the multiplications required for obtaining squares, ultimately propagating through to 3.
The execution of the quantum circuit would yield a joint superposition of possible outcomes, revealing not just individual results for values of (f(x))—such as (0^2=0), (1^2=1), (2^2=4), and (3^2=9)—but also the cumulative probabilities of various results manifesting as we measure the quantum states at the completion of our operations. In quantum computing, measurement collapses the quantum superposition into one probabilistic outcome, directing attention towards the most likely results.
To glean insights into the efficacy of our calculation, one must consider not just the computed results but also the unique potential of qubits to solve these problems at an unprecedented scale. Quantum algorithms can leverage parallelism through intrinsic state overlaps, thereby solving problems much faster than classical analogs.
Nonetheless, the implementation of quantum calculations introduces a host of complexities that stem from both technological constraints and algorithmic precision. Quantum decoherence and noise perturbations challenge the fidelity of qubit states, necessitating robust error correction methods. Moreover, the optimization of quantum circuits remains an expansive area of inquiry, driving researchers toward more sophisticated quantum algorithms capable of addressing diverse computational challenges.
In conclusion, making a simple calculation with qubits may provide the glimpse of a profound paradigm shift in computation. The quintessence of this inquiry illuminates not only the mechanics of utilizing qubits but also highlights the vast opportunities awaiting exploration where classical limitations give way to the endless potential imbued in quantum phenomena. As one reflects on the playful challenges of this quantum journey, it becomes clear that unraveling the utility of qubits transcends mere calculations, beckoning a revolution in data processing and algorithmic comprehension.