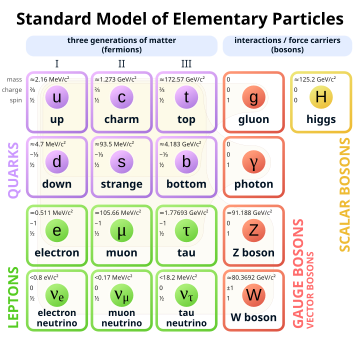
In the realm of particle physics, the term “hermeticity” emerges as a pivotal concept steeped in complexity and significance. Although often relegated to the periphery of public discourse, hermeticity encapsulates essential principles that govern the behavior of particles and fields at a fundamental level. This article delves into the nuances of hermeticity, its implications for the conservation of quantum states, and its striking connections to broader themes in modern physics.
At its core, hermeticity pertains to the mathematical structure of quantum systems. Specifically, it relates to the hermitian nature of operators that describe physical observables. In quantum mechanics, physical observables—such as position, momentum, and energy—are represented by operators, and these operators must satisfy certain criteria to yield meaningful results. A hermitian operator is one that is equal to its own adjoint, a property that guarantees real eigenvalues and ensures that measured quantities correspond to observable phenomena.
The significance of hermitic operators cannot be overstated. The requirement for observables to be hermitian underlines a fundamental tenet of quantum mechanics: the need for measurable predictions to be real numbers. This profound relationship solidifies the foundation of mathematical physics, ensuring that when particles are observed, the outcomes are empirically viable. Thus, the concept of hermeticity underpins the verification and validation of experimental results in particle physics.
Moreover, hermeticity is intricately linked to the conservation laws that permeate the universe. When we consider a closed quantum system, hermeticity implies that the evolution of the system is deterministic and reversible, governed by the Schrödinger equation. This characteristic is quintessential for the conservation of probability, which is paramount in quantum theory. The interplay of these elements suggests a stringent framework within which particle interactions and transformations occur. In essence, if a system is hermitian, it cannot spontaneously decay into non-hermitian forms, preserving the integrity of quantum states over time.
Another critical dimension of hermeticity lies in its implications for symmetries. In particle physics, symmetries dictate the interactions and behaviors of particles under various transformations. For instance, the principle of invariance under certain operations leads to conservation laws like charge conservation and lepton number conservation. Hermeticity ensures that these symmetries are upheld in quantum mechanical processes, leading to a deeper understanding of the fundamental interactions that shape our universe.
On an intuitive level, addressing the notion of hermeticity also resonates with a fascination that scientists and lay observers share alike: the enigmatic nature of reality itself. The transition from classical determinism to quantum indeterminacy can be perceived as a microscopic hermetic seal. Just as a hermetic container prevents the ingress of external influences, hermeticity in quantum mechanics delineates boundaries where measurable phenomena exist distinct from the chaotic stimulus of the external world.
This contemplation raises intriguing questions surrounding the nature of reality. If hermeticity provides a framework for a closed system’s behavior, what of the interactions with the external environment? The introduction of non-hermitian operators, which may describe open quantum systems, invites a discourse on the limits of hermeticity. Non-hermitian interactions reveal how particles can enter or exit a given state, introducing the concept of decoherence. This inherently non-hermitian behavior elucidates the transition from quantum superposition to classical outcomes, bridging the gap between the microscopic and macroscopic worlds.
Within experimental physics, the principle of hermeticity manifests itself in various ways. For instance, in high-energy particle colliders, enhancing the hermeticity of detector systems ensures that the collected data accurately represent the phenomena occurring during collisions. Such measures are crucial in minimizing the effects of external noise and interference, leading to cleaner experimental results. The meticulous engineering of these hermetic systems reaffirms the notion that the pursuit of knowledge is as much about precision as it is about inquiry.
Furthermore, hermeticity can be leveraged in the development of innovative technologies, such as quantum computing and quantum cryptography. Here, engineers strive to create hermetic environments where quantum states can be manipulated without succumbing to decoherence, thereby harnessing the power of quantum superposition for computational advantages. The very essence of hermeticity becomes a tool for technological advancement, breeding new methodologies that could redefine our computational landscape.
The concept of hermeticity, with its mathematical and philosophical ramifications, serves as a profound gateway to understanding the intricate tapestry of particle physics. Its connection to the fundamental nature of quantum mechanics, conservation laws, symmetries, and the dichotomy between predictability and chaos elucidates a field rife with complexities yet grounded in essential principles. The sheer beauty of hermeticity lies not only in its analytical rigor but also in its ability to inspire curiosity about the universe’s underpinnings, inviting scientists and scholars to persist in their ongoing voyage of discovery.
As we continue to unravel the mysteries within the quantum realm, the notion of hermeticity will undoubtedly remain a focal point of inquiry, revealing not just the mathematical elegance of nature, but also its profound and, at times, unfathomable depth. Such explorations promise to deepen our understanding not solely of particles and forces, but of reality itself, encapsulated within a framework where the observable converges with the theoretically profound.