Molecular orbital theory (MOT) stands as a monumental progression in the field of quantum chemistry, offering insights that transcend the limitations of the Bohr model. As an endeavor to understand how electrons are arranged in atoms and molecules, MOT challenges us to ponder: can the behavior of electrons in molecules truly be captured by simple orbits, or do we need a more nuanced framework that accommodates the complexities of chemical bonding?
The dichotomy between atomic and molecular structures forms the foundation of MOT. While the Bohr model provides an excellent introduction for isolated atoms—depicting electrons as particles moving in discrete orbits around a nucleus—it falters when it comes to explaining molecular interactions. The necessity to account for phenomena such as resonance, delocalization, and hybridization of atomic orbitals unveils a world of complexity that requires deeper theoretical underpinnings.
At its core, molecular orbital theory proposes that, in a molecule, atomic orbitals combine to form molecular orbitals. These orbitals are not localized around individual nuclei but rather extend over the entire molecule, reflecting the delocalization of electrons. To grasp this concept, one must engage with the notions of constructive and destructive interference, where overlapping atomic orbitals can write the story of how covalent bonds are formed—or, conversely, how they may fail to exist.
The formation of molecular orbitals occurs through a process known as linear combination of atomic orbitals (LCAO). Here, the wave functions of atomic orbitals from participating atoms are mathematically summed to create combinations that can be occupied by electrons. Two principal types of molecular orbitals emerge from this process: bonding orbitals, which result from the constructive interference (where wave functions reinforce each other), and antibonding orbitals, arising from destructive interference (where wave functions cancel each other out).
Let us consider diatomic hydrogen (H2). The individual hydrogen atoms, each possessing a single electron in their 1s orbital, demonstrate a striking transformation when they approach each other. According to MOT, as these atomic orbitals converge, they produce a sigma (σ) bonding molecular orbital, lower in energy than the constituent atomic orbitals. This synergy decreases the energy of the system, resulting in a stable bond. Conversely, the creation of the antibonding molecular orbital (σ*) represents a state of higher energy, indicating that occupancy here would disrupt the bond.
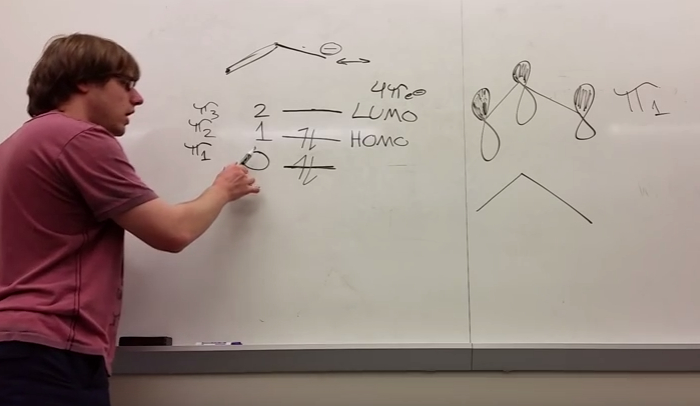
As we delve deeper into molecular orbital theory, it becomes evident that electron distribution is intrinsically tied to energy levels. The Aufbau principle prescribes the manner in which electrons fill molecular orbitals, beginning with the lowest energy and proceeding towards higher levels. For example, in a homonuclear diatomic molecule like nitrogen (N2), the orbital energy level diagram elucidates the filling of the σ(1s), σ*(1s), σ(2s), σ(2s)*, and σ(2p)z orbitals before the π(2p)x and π(2p)y orbitals. This systematic filling imparts insights into molecular stability and magnetic properties, elucidated through the manifesting of unpaired electrons.
Interestingly, MOT also affords a robust framework for interpreting the magnetic characteristics of molecules. Diamagnetism—characterized by the absence of unpaired electrons—contrasts starkly with paramagnetism, which emerges in the presence of unpaired electrons. Therefore, the spectroscopic behavior of a molecule can be mapped against the presence or absence of these electrons, guiding chemists in predicting molecular reactivity and properties.
The implications of molecular orbital theory extend beyond simple diatomic molecules, embracing more complex species as well. When analyzing polyatomic molecules, the combination of atomic orbitals leads to the emergence of molecular orbital diagrams that depict various overlap geometries, ultimately influencing molecular geometry and hybridization. The concept of hybridization—a critical advancement inherent in the framework of MOT—integrates the characteristics of various atomic orbitals to develop new, equivalent orbitals for bonding purposes. For example, in methane (CH4), the sp3 hybridization allows for an optimal four equivalent orbitals to arrange tetrahedrally around the carbon nucleus.
Yet, challenges persist when attempting to apply molecular orbital theory to larger and more complex molecules. The onset of computational chemistry presents a solution to these challenges, and methods such as density functional theory (DFT) and Hartree-Fock calculations epitomize modern advances in accurately predicting molecular behavior and properties through sophisticated algorithms. These methodologies allow chemists to tackle the complexities of large molecules that could defy even the most detailed applications of MOT.
In conclusion, molecular orbital theory orchestrates a transformative approach to understanding chemical bonding that reveals the limitations of the Bohr model. By embracing the principles of wave mechanics, delocalization, and hybridization, MOT furnishes a compelling narrative of molecular interactions. As students and researchers venture into this realm, they are poised not only to appreciate the elegance of molecular structures but also to grapple with the challenges of interpreting increasingly complex systems. Thus, the journey through molecular orbitals unveils a magnificent tapestry of chemical phenomena waiting to be unraveled.