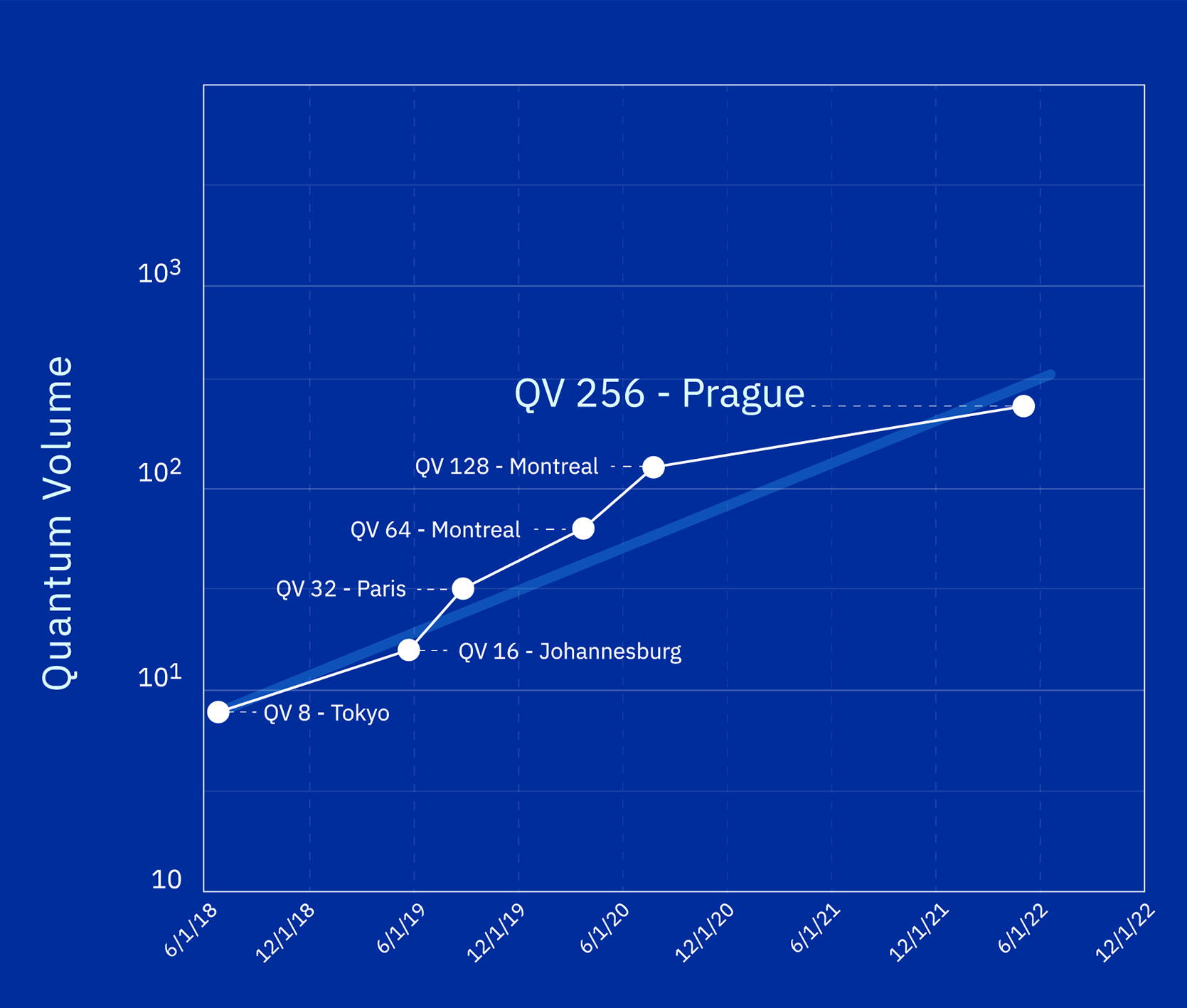
Quantum computing has evoked a profound fascination within both scientific and technological communities, primarily because of its potential to revolutionize problem-solving methodologies across diverse disciplines. A pivotal concept in assessing the capabilities of quantum computers is the quantum volume score. This metric serves as a guiding beacon, helping researchers and practitioners evaluate the performance and utility of quantum systems in practical applications. Understanding the quantum volume score requires delving into the intricacies of quantum gates, coherence times, and physical qubits’ arrangements, all of which contribute to the overall efficacy of quantum computations.
To embark on this exploration, it is imperative first to comprehend the foundational aspects of quantum computing. At its core, quantum computing harnesses the principles of quantum mechanics to process information in fundamentally different ways compared to classical computing paradigms. Classical bits, the fundamental units of computer information, exist in states of 0 or 1. In contrast, qubits, the building blocks of quantum information, can exist in superpositions of states, allowing for an exponential increase in computational capacity. Thus, the potential for enhanced processing power is immense, yet highly dependent on the design and scalability of the quantum architecture constructed.
The quantum volume score encapsulates the multifaceted capabilities of a quantum computing system into a singular evaluative metric. The score merges multiple dimensions of quantum performance, including the number of qubits, gate fidelity, and circuit depth. Each of these components plays a critical role in determining how effectively a quantum computer can execute algorithms. For instance, while having a larger number of qubits can intuitively suggest a greater processing ability, it is not adequate if those qubits lack coherence or if the gates connecting them exhibit low fidelity.
Exploring the mathematical formulation of quantum volume reveals its intricate design. It is expressed as:
Quantum Volume = 2^a
In this equation, ‘a’ is determined by the minimum of the number of qubits and the maximum circuit depth that can be reliably executed based on the fidelity of operations. This dual dependency highlights the trade-offs inherent in quantum system design: optimizing for qubit quantity could impose constraints on operational fidelity, and vice versa. Thus, the quantum volume score is not merely a reflection of size, but rather indicates the practical computational power available within existing operational parameters.
The significance of quantum volume score transcends the realm of numerical representation; it serves as a tangible benchmark for the progress of quantum technology. In this way, it brings forth a common observation in the field: merely increasing the number of qubits does not equate to more effective quantum computing. There is a delicate balance that needs to be maintained between qubit count, the interconnectivity of those qubits, and the execution fidelity of quantum gates. As researchers embark on developing more advanced quantum computers, they invariably grapple with the challenge of scaling quantum volume without sacrificing other critical performance metrics.
This leads to the question: Why does the quantum volume score elicit so much intrigue within the scientific community? One contributing factor lies in the palpable potential for quantum computing to solve problems that are currently insurmountable for classical computers. Quantum volume, therefore, acts as an indicator of the viability of such solutions. For example, the advent of quantum algorithms such as Shor’s and Grover’s algorithms lays claim to exponentially faster computation for specific problems. The desire to harness the full promise of these algorithms drives the need for improved quantum volume in quantum systems.
Moreover, the notion of quantum volume invites discourse about the intricate balance between theoretical constructs and practical implementations. As quantum technologies proliferate and become more accessible, researchers are challenged to bridge the gap between theoretical capabilities and tangible results. This interplay of theory and application not only fuels scientific inquiry but also bridges diverse fields including cryptography, materials science, and complex system modeling.
Furthermore, quantifying the progress of quantum technologies through the lens of quantum volume facilitates effective comparisons between different quantum architectures. This interdisciplinary aspect of quantum volume assessment is crucial as it integrates facets from quantum mechanics, computer science, and engineering, fostering collaborations that can propel the field forward. By employing quantum volume as a reference point, stakeholders can engage in discursive analysis on factors that can be optimized to achieve higher computation efficiencies.
As researchers continue to innovate in quantum chip design and error-correction techniques, the quantum volume score will undoubtedly evolve, reflecting the most recent advancements in the field. This open-ended nature of quantum volume underscores the dynamic character of quantum computing research. Iterative improvements will lead to transformative developments, propelling the quantum volume score not only as a numeral, but as an intellectual emblem of progress.
In conclusion, the quantum volume score stands as a cornerstone of understanding the landscape of quantum computing. Its multifaceted nature encapsulates the potential and limitations of quantum systems and serves as an auditor of their efficacy in addressing computational challenges. The quest for higher quantum volume is a reflection of a larger narrative within the scientific community, one fueled by an insatiable desire to unlock the seemingly limitless capabilities of quantum mechanics. As curiosity fuels inquiry and technological advancements pave the way forward, the quantum volume score remains a critical measure of our ever-evolving understanding of this fascinating frontier.