The Kondo problem stands as a conundrum within the realm of condensed matter physics, raising questions about the interactions between localized magnetic moments and conduction electrons in metallic systems. How do we reconcile our understanding of localized magnetic states with the complexity of electron interactions at low temperatures? This question not only speaks to the core of theoretical physics but also hints at the intricate tapestry of phenomena that characterize both solid-state physics and quantum mechanics.
At its inception, the Kondo problem originates from observations in the 1960s concerning the electrical resistivity of certain metals containing magnetic impurities. When diluted with non-magnetic hosts, these impurities were found to increase resistance as temperature decreased, counterintuitive to expectations rooted in conventional metallic behavior. Did not the resistivity typically diminish with lowering temperatures due to decreased lattice vibrations? This curious behavior illustrated the emergence of what would become known as the Kondo effect.
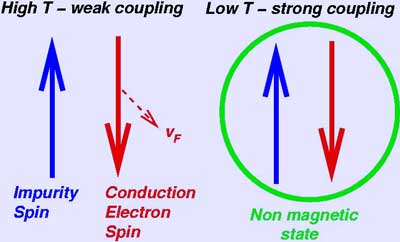
The Kondo effect manifests when an individual magnetic impurity—often characterized by a spin—couples to the surrounding sea of conduction electrons. This interaction leads to an anomalous temperature-dependent resistivity: the electron scattering off the magnetic moment increases at lower temperatures. This phenomenon is non-trivial, demanding a rigorous examination through many-body physics and quantum field theories.
Mathematically, the Kondo problem is represented through the Kondo Hamiltonian, which encapsulates the spin interactions within the conduction electron system. This Hamiltonian typically consists of three main components: a kinetic term that describes the conduction electrons, a term that embodies the impurity’s localized moments, and a coupling term that embodies the interaction between the two. Such a model necessitates a treatment beyond simple perturbation theory, indicating a deep non-linear interaction and the emergence of non-trivial ground states.
As we delve deeper into this realm, one encounters critical notions such as screening and the emergence of the Kondo resonance. When a conduction electron approaches a magnetic impurity, its spin can align or anti-align with the impurity’s spin due to the exchange interaction characterized by the Kondo coupling constant. As this interaction continues, a many-body effect emerges, where the impurity’s magnetic moment becomes screened by the surrounding electrons, resulting in an effective reduction of the localized moment at low temperatures.
The Kondo effect can be illustrated through the temperature dependence of resistivity. At elevated temperatures, the scattering off the magnetic moment is negligible, leading to conventional metallic behavior with a decrease in resistance. However, as the temperature declines towards the Kondo temperature, a distinctive crossover occurs. Instead of continuing to decrease, the resistivity rises, revealing the presence of the Kondo resonance—a sharp peak in the density of states at the Fermi energy, which dominates the low-temperature physics of the system.
Yet, this seemingly straightforward manifestation of the Kondo effect belies deeper complexities. The Kondo problem extends into realms that necessitate advanced theoretical frameworks like renormalization group analysis and numerical renormalization group (NRG) methods, which provide profound insights into its many-body interactions. Notably, the NRG has become a quintessential tool in tackling the Kondo problem, enabling physicists to probe the system’s behavior across numerous scales and connect microscopic interactions to macroscopic observables.
The Kondo problem does not rest solely within the boundaries of static systems; dynamic perturbations significantly affect the implications of Kondo physics. For instance, when subjected to external magnetic fields or additional interactions, the Kondo effect illustrates phase transitions and even reflects properties relevant to quantum criticality. Furthermore, variations such as the multi-channel Kondo effect arise when multiple independent channels of conduction electrons couple to a single magnetic impurity, resulting in complex behavior marked by richer topology and collective phenomena.
In addition to the single impurity model, researchers have extended Kondo physics to accommodate systems with multiple magnetic impurities, leading to the exploration of the Kondo lattice model. This paradigm transitions from a localized spin interacting with conduction electrons to a whole lattice of magnetic moments interacting via RKKY interactions. This model crucially underscores how inter-impurity interactions can induce novel states, such as heavy fermion behavior, emerging from the interplay of magnetic order and charge transport.
Furthermore, the Kondo problem has profound implications extending beyond metals into experimental realms such as quantum dots and nanostructured materials. In these systems, the tunability of parameters like coupling strength and temperature facilitates a rich landscape of Kondo physics that can be experimentally probed. Consider, for example, a quantum dot with a single magnetic impurity: tuning the gate voltage allows for exquisite control over the system, leading to a plethora of phenomena that reflect the intricate dance of quantum mechanics. This adaptability has paved the way for potential applications in quantum computing, where managing quantum states is vital for information processing.
In conclusion, the Kondo problem encapsulates the richness and complexity inherent in condensed matter physics, challenging us to rethink our intuitions about order, disorder, and electron interactions. The interplay of localized spins with a sea of conduction electrons not only informs our understanding of resistivity but also lays the foundation for exploring novel states of matter emerging from strong correlations. As we forge ahead in our inquiry into this fascinating domain, the Kondo problem will undoubtedly continue to provide insights into the intricate behaviors that govern the quantum world.