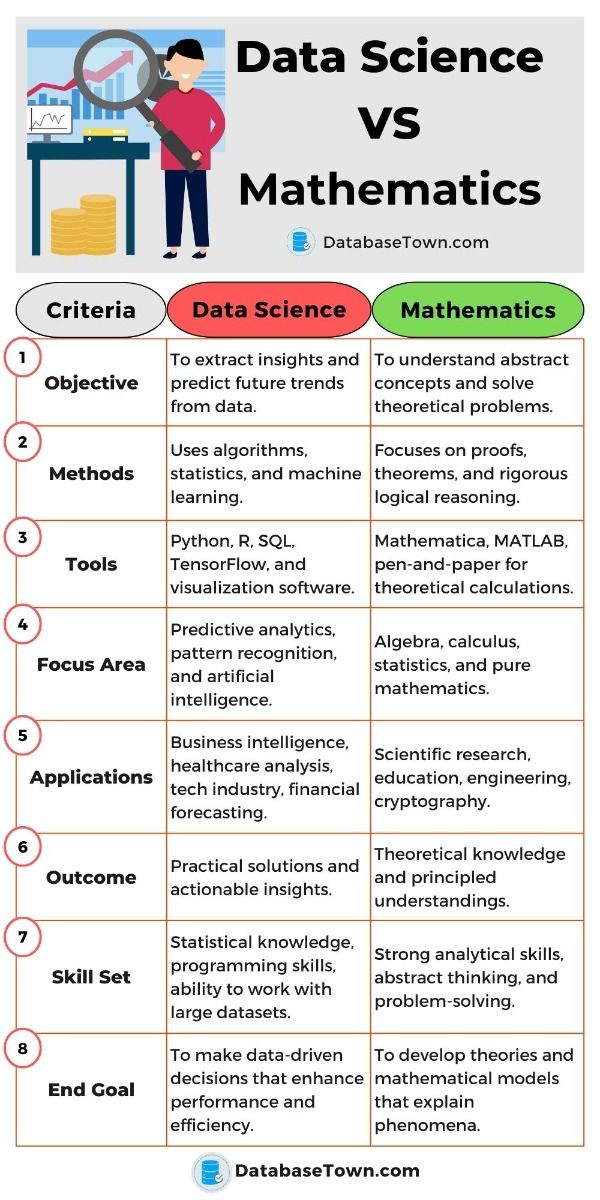
Understanding the differences between mathematics and computer science is vital for students, educators, and professionals in the fields of technology, science, and engineering. At a superficial level, both disciplines may appear interconnected, yet they diverge significantly in their methodologies, applications, and underlying philosophies. This article endeavors to elucidate the salient differences between the realms of mathematics and computer science through several dimensions, ultimately assisting readers in comprehending the unique essence of each discipline.
1. Fundamental Nature and Origin
Mathematics is traditionally rooted in the exploration of abstract concepts, structures, and relationships. It originated as a tool for quantifying and understanding the natural world, evolving through centuries of rigorous logical reasoning and theorization. At its core, mathematics seeks to establish universal truths through axioms and theorems, often focusing on proof-based methodologies.
Conversely, computer science is a relatively recent discipline that emerged in the mid-20th century, catalyzed by the advent of electronic computers. It encompasses the study of algorithms, computational processes, and data structures. While mathematics serves as a theoretical underpinning for some aspects of computer science, the latter is primarily concerned with practical implementation and problem-solving within real-world contexts.
2. Areas of Focus and Theoretical Constructs
Mathematics is broadly classified into various domains, including algebra, calculus, topology, and number theory. Each of these areas addresses abstract concepts and leads to further theoretical exploration without necessarily demanding practical applications. For instance, topology examines properties of space that remain invariant under continuous transformations, while number theory delves into the intrinsic nature of integers.
On the other hand, computer science encompasses a diverse array of subfields such as algorithms, programming languages, artificial intelligence, and hardware architectures. These areas often incorporate mathematical principles but prioritize their practical applicability. The study of algorithms, for instance, hinges on efficiency and optimization—attributes that transcend the abstract nature typically found in pure mathematics.
3. Methodologies and Problem-Solving Techniques
The methodologies employed by mathematicians and computer scientists delineate further distinctions between the two fields. Mathematicians often engage in deductive reasoning, enhancing their propositions through rigorous proof and counterexamples. Their work frequently culminates in the establishment of generalized theories applicable across numerous scenarios.
Conversely, problem-solving in computer science frequently employs a blend of both inductive and deductive methodologies. While theoretical proofs are crucial, computer scientists often prioritize experimental validation and practical applications of algorithms or systems. This methodology not only addresses theoretical constructs but also ensures that solutions are viable and efficient in real-world applications.
4. Applications in Industry and Research
The applications of mathematics are diverse and far-reaching, affecting fields such as physics, engineering, finance, and economics. Mathematicians might model phenomena such as population growth or the behavior of particles under various conditions, employing their abstract theories to facilitate concrete understanding in these applied domains.
Conversely, computer science has revolutionized industries through its rapid technological advancements. Software development, cybersecurity, data analysis, and machine learning are some examples where computer science principles are applied to innovate and enhance operational efficiencies. Professional roles such as software engineers, data scientists, and systems analysts illustrate how computer science extends well beyond the theoretical realm, impacting everyday technological experiences.
5. Educational Pathways and Skill Acquisition
The educational pathways leading to careers in mathematics and computer science further emphasize the differences between the disciplines. Mathematics programs generally focus on analytical skills, rigorous proof construction, and explorations of theoretical frameworks. Through coursework and advanced studies, students cultivate an exquisite mastery of logical reasoning and abstract thinking.
In contrast, computer science education often integrates practical experience with theoretical principles. Students typically engage with programming languages, software development, and system design, emphasizing both the construction and evaluation of technical solutions. Skills such as coding, algorithm design, and system architecture become paramount in this vocation, distinguishing it significantly from the core competencies emphasized in mathematics.
6. Interdisciplinary Synergy and Collaboration
Despite the distinctions, mathematics and computer science share a profound synergy that has led to numerous interdisciplinary collaborations. Mathematical foundations such as discrete mathematics, linear algebra, and probability theory are instrumental in advancing computational theories and practices. This blend fosters the development of new algorithms, optimizations, and computational methodologies.
Moreover, contemporary fields like data science and machine learning epitomize this collaboration, where mathematical principles are fundamentally intertwined with computational strategies. These interdisciplinary areas highlight the necessity of proficiency in both fields to tackle complex, data-driven challenges effectively.
Conclusion
In summary, while mathematics and computer science bear some similarities, they are distinct disciplines characterized by unique methodologies, areas of focus, and applications. Mathematics thrives in the realm of abstraction and theoretical inquiry, while computer science orbits around practical implementations and technological applicability. As society continues to evolve technologically, a comprehensive understanding of both fields will remain crucial for advancing academic, professional, and interdisciplinary endeavors.