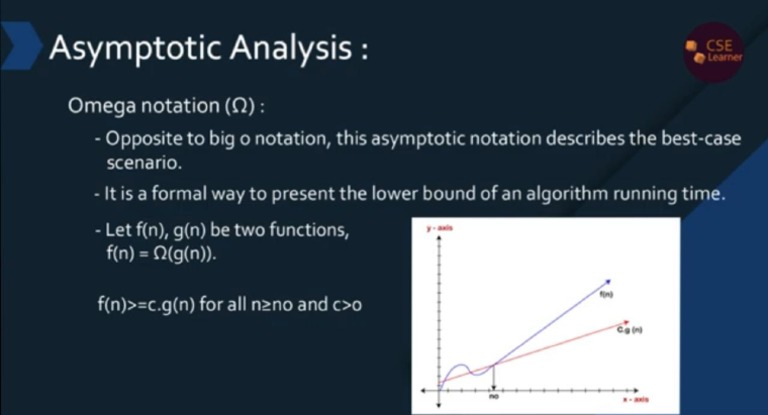
Asymptotic freedom is a pivotal concept in quantum chromodynamics (QCD), which describes the behavior of the strong force—the fundamental interaction that holds quarks and gluons together to form protons and neutrons. This phenomenon refers to the intriguing property of certain gauge theories, particularly those involving asymptotic states of particles at high energies or short distances. The term was first introduced in the context of QCD and represents a departure from conventional understandings of force interactions.
To appreciate the depth of asymptotic freedom, one must first delve into the historical context of particle physics. The discovery of asymptotic freedom emerged during an era marked by the quest to unify the fundamental forces of nature. In the late 20th century, David Gross, Frank Wilczek, and H. David Politzer introduced the concept, fundamentally reshaping our comprehension of strong interactions.
At the heart of asymptotic freedom lies the coupling constant, which quantifies the strength of interaction between particles. In conventional scenarios, one would expect that, as particles come closer to each other, they experience an increasing force. However, in the case of QCD, the coupling constant diminishes as the separation between quarks becomes infinitesimal. This counterintuitive behavior implies that quarks interact weakly at extremely short distances, a property that starkly contrasts with the behavior of electromagnetic forces.
Asymptotic freedom can be explicated through the concept of the renormalization group, a mathematical framework that explores how physical parameters change with varying energy scales. As particles—specifically quarks—approach proximity, their effective interactions become weaker. This renormalization process elucidates why quarks remain ‘free’ at high energies, yet become confined within hadrons at lower energies. The concept leads to the notion of confinement, another fundamental aspect of QCD, postulating that quarks cannot exist independently in low-energy states.
The interaction strength can also be explored through diagrams known as Feynman diagrams, which offer visual representation of particle interactions. In QCD, the gluons are responsible for transmitting the strong force, visibly demonstrating the intricate dance of quarks and gluons. Unlike photons in electromagnetic interactions, which interact less strongly at increased distances, gluons exhibit strong self-interactions at larger scales, contributing to the non-abelian nature of QCD. This complexity further enriches the understanding of asymptotic freedom.
One cannot discuss asymptotic freedom without addressing the significance it holds for the broader landscape of particle physics. Particularly, this concept provides foundational insights into the behavior of hadrons, paving the way for experimental investigations in high-energy physics. Understanding the dynamics at play in deeply inelastic scattering experiments, for example, reveals how asymptotic freedom manifests in practical applications. In these high-energy collisions, quarks behave as nearly non-interacting particles, facilitating measurements that would be otherwise unattainable.
The experimental confirmations of asymptotic freedom have profound implications. The discovery of jets in deep inelastic scattering experiments, where quarks were observed to behave as free particles within high-energy collisions, serves as resounding evidence of this phenomenon. Such findings affirm the predictions made by theoretical models of QCD, subsequently bolstering the Standard Model of particle physics.
Asymptotic freedom also provides a framework for understanding the early universe’s conditions, particularly during the quark-gluon plasma phase. In the moments following the Big Bang, temperatures were extraordinarily high, enabling quarks and gluons to exist as a free state, effectively redefining the nature of matter at that epoch. This transition from a plasma state to a confining state as the universe cooled has ramifications that extend to cosmological models and our understanding of the universe’s evolution.
However, while asymptotic freedom is a cornerstone of theoretical physics, several challenges remain. The conundrum of confinement—an oppositely contrasting phenomenon—is still a subject of vigorous research. Despite the theoretical underpinnings provided by lattice QCD and other computational approaches, a comprehensive understanding of why quarks cannot exist independently in low-energy scenarios remains elusive. This paradox invites physicists to delve deeper into the fabric of the universe, searching for innovative resolutions.
Furthermore, asymptotic freedom is not confined to QCD alone. It serves as a prototype that can be extrapolated to other gauge theories, where similar behaviors may emerge under varying circumstances. The universality of this principle invites parallel explorations in condensed matter physics, cosmology, and beyond, increasingly integrating diverse fields of study into a cohesive tapestry of theoretical exploration.
In conclusion, asymptotic freedom is not merely a defining trait of QCD; it encapsulates a fundamental paradigm that reshapes our understanding of particle interactions. As one navigates through the complexities of this concept, an intricate picture emerges—one that interlaces theory, experiment, and cosmological implications into a unified narrative. As research progresses, continued investigations into the ramifications of asymptotic freedom will likely yield further revelations, shedding light on one of the most mysterious aspects of our physical universe.