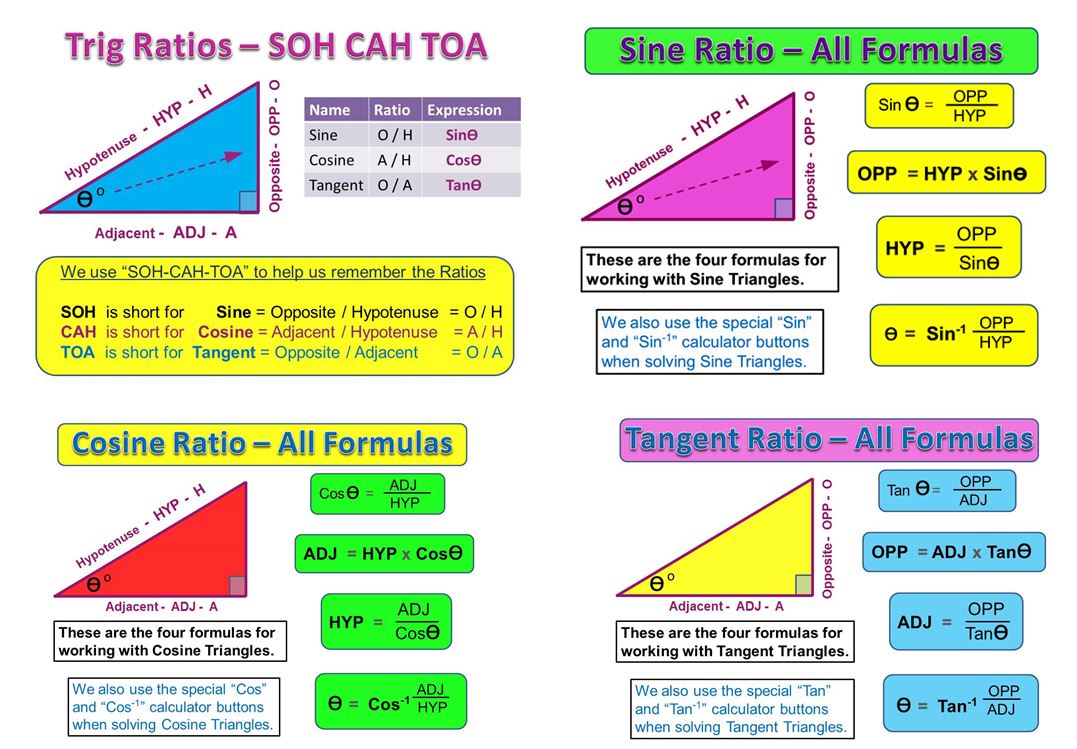
Trigonometry, commonly perceived as a branch of mathematics primarily pertinent to triangles and periodic phenomena, finds its essential utility in numerous scientific domains. Among these, nuclear physics stands out as a field where the geometric intricacies of trigonometric principles are not merely beneficial; they are foundational. Understanding the pervasive role of trigonometry in nuclear physics invites a novel perspective that bridges mathematical theory and practical application.
The relationship between nuclear physics and trigonometry is intricate, beginning with the fundamental necessity of angular measurements in various nuclear processes. Nuclear reactions, which occur when atomic nuclei collide, transform, or decay, involve particles that traverse complex paths through space. The trajectories of these particles are pivotal, a phenomenon dictated by both their energy and the angles at which they interact. In this context, trigonometric functions like sine, cosine, and tangent become invaluable tools for calculating distances, angles, and the resultant motion of particles.
At a macroscopic level, one of the most pronounced applications of trigonometry in nuclear physics is in the precise measurements of radiation. Detectors position themselves at calculated angles to ascertain the intensity and type of radiation emitted by a source. This geometric positioning is paramount; specific angular alignments maximize detection efficiency and accuracy, ensuring reliable measurements vital for research and safety protocols. Here, the application of sine and cosine laws facilitates the interpretation of data by enabling physicists to decompose vectors describing radiation into orthogonal components, leading to clearer insights into the dynamics of nuclear events.
Furthermore, within the realm of particle accelerators, trigonometry plays a crucial role in optimizing the trajectories of particles. Nuclear physicists utilize powerful accelerators to propel charged particles at relativistic speeds. The design of these accelerators relies on precise calculations of angles and distances between magnetic fields and particle beams. Lessons learned from trigonometric relationships help physicists ascertain how deviations from intended paths occur, which is essential in maximizing collision rates and enhancing experimental outcomes.
Conversely, as one delves deeper into subatomic interactions, the role of trigonometry becomes even more pronounced. Nuclear decay processes, such as alpha and beta decay, often release particles at specific emission angles relative to the original nucleus. The azimuthal and polar distributions of these emissions can be modeled using spherical coordinates, wherein trigonometric functions help represent the complex relationships between parameters like energy, momentum, and kinetic angles. Without the mathematical framework provided by trigonometry, predicting particle behavior in these decay processes would prove exceedingly cumbersome and inaccurate.
Moreover, nuclear fusion, a process that fuels stars including our sun, heavily employs trigonometric models. In fusion reactions, the precise alignment of nuclei is critical to achieve the conditions under which they overcome electromagnetic repulsion and fuse. The probability of fusion occurring often hinges upon the relative angles of approach of colliding nuclei, a factor that can be quantitatively analyzed using trigonometric concepts. Understanding these angles can enhance efforts in achieving controlled fusion conditions on Earth, thus promising vast energy potentials.
A profound implication of these considerations resides in the realm of quantum mechanics, where the wave-particle duality of subatomic entities presents an additional layer of complexity. The probabilistic nature of waves necessitates the use of trigonometric functions to describe the behavior of particles effectively. The wave functions that characterize particles in a nuclear context often employing sine and cosine functions form the backbone of quantum mechanics. These functions delineate the probability amplitudes of finding a particle in a certain state or position, and are inherently linked to spatial configurations described by angular coordinates.
As we extend our inquiry, it becomes clear that trigonometry also aids in the visual representation of nuclear phenomena. The graphical interpretation of nuclear interactions utilizes three-dimensional representations where the practical aspects of trigonometry help articulate phenomena that otherwise remain abstract. Such visualizations contribute significantly to the communication of complex concepts to a broader audience, emphasizing the role of mathematics in elucidating the nuances of physical interactions.
The relationship between trigonometry and nuclear physics thus unfolds as a captivating tapestry, woven through principles of geometry, angular dynamics, and wave mechanics. Each thread signifies a unique application or insight, collectively enhancing our comprehension of nuclear interactions. As physicists continue to explore the mysteries of the atomic nucleus, the robust foundation laid by trigonometric principles promises not only to illuminate the processes of nuclear physics but also to inspire future innovations in energy production and nuclear technology.
In conclusion, the revelation of trigonometry as an indispensable ally in the realm of nuclear physics serves to enrich our appreciation of mathematics as a universal language. In its intricate dance with the laws of physics, trigonometry does not merely provide computational support; it offers a completely different lens through which to view the natural world. This peculiar interplay urges us to recognize the elegance of physics in all its dimensions and complexities, enticing curiosity and fostering deeper understanding.