The realm of theoretical physics is often replete with abstract concepts and intricate symmetries, yet few have elicited as much excitement and scholarly inquiry as the E8 symmetry. The recent observation of E8 symmetry in ultracold magnetic systems heralds a new chapter in our understanding of high-energy physics, condensed matter, and the underlying universal principles that govern the behavior of matter at the quantum level. To unpack the significance and implications of this discovery, one must first traverse the intricate landscape of both E8 symmetry and the fascinating properties of ultracold magnets.
At its core, E8 is a structure belonging to the domain of Lie groups and algebraic geometry. It is characterized as one of the most complex and symmetrical objects known to mathematicians, containing 248 dimensions. The classification of E8 resides within a broader hierarchy of Lie groups, which serve as vital frameworks for understanding symmetries in mathematical physics. These groups encapsulate the diverse behaviors of particles and forces, revealing deep connections between seemingly disparate physical phenomena.
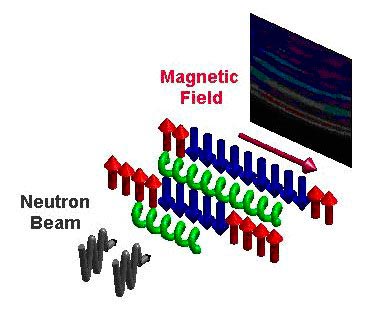
Ultracold magnets, on the other hand, represent a subclass of materials that exhibit unique magnetic properties at temperatures near absolute zero, where thermal fluctuations are suppressed. In this regime, quantum mechanical effects become pronounced, allowing researchers to explore phenomena such as quantum entanglement and spin interactions in unprecedented detail. The interplay of magnetic interactions and quantum mechanics in ultracold environments facilitates the manifestation of exotic phases of matter, including spin liquids and topological states.
The recent identification of E8 symmetry in ultracold magnet systems has crucial implications across multiple facets of theoretical and applied physics. This conflation suggests that these magnetic materials may serve as a bridge between abstract mathematical constructs and tangible physical environments, enabling deeper insights into the nature of reality. Notably, this advancement could catalyze progress in areas such as quantum computing, where the stability and coherence of qubits are paramount.
Central to the manifestation of E8 symmetry in ultracold magnets is the concept of magnetic ordering and the emergence of a ground state, which is dictated by the interactions between the magnetic moments of the constituent particles. In systems adhering to E8 symmetry, one witnesses intricate patterns of affined group dynamics, where the magnetic order is not simply localized but rather extends across the entirety of the system, fundamentally redefining our understanding of magnetic interactions. This global ordering phenomenon calls forth a plethora of magnetically ordered states, effectively elucidating how E8 symmetry facilitates the coexistence of multiple magnetic phases.
The interplay between temperature and magnetic fluctuations further nuances the investigation of E8 symmetry in ultracold settings. In the vicinity of a critical phase transition, intricate fluctuations emerge as thermal energy induces complex magnetic arrangements. This phenomenon appears strikingly resonant with the properties of E8, wherein symmetry ensures stability against perturbations, providing a fertile ground for many-body interactions to flourish. Recognizing such a framework not only enhances theoretical models but also implicates experimental predicaments en route to practical realizations of highly symmetric materials.
Moreover, this development invites inquiries into the manifestation of E8 across different realms, extending its relevance beyond condensed matter physics. The potential unification of forces—a tantalizing prospect in theoretical physics—could well hinge upon the attributes of symmetries, like that of E8, in high-energy environments. Such investigations may elucidate the structuring of spacetime at cosmological scales, affording a unified perspective that minimizes discrepancies between general relativity and quantum mechanics.
Examining the empirical facets of this inquiry contributes significantly to our understanding of E8 symmetry in ultracold magnets. Specific experimental setups utilizing optical lattices or magnetic traps allow the precise control of external parameters to tune the magnetic interactions and investigate the emergent phenomena linked with E8. Through precise measurements of the associated observables—ranging from magnetization to susceptibility—researchers can discern the signature characteristics of E8 symmetry under varying external conditions. This intricate experimental paradigm underscores the compelling unity between theoretical constructs and experimental realities.
Furthermore, the implications of E8 symmetry transcend its intrinsic beauty; they open new avenues for technological innovation. In the domain of quantum information processing, materials exhibiting E8 symmetry may host highly localized zero-energy states, which can bolster fault-tolerant quantum computation by stabilizing qubit configurations. This integration of advanced materials into quantum circuits pioneers novel applications in computing and information retrieval, thereby harnessing the complex interplay of symmetry and magnetism.
In conclusion, the observation of E8 symmetry in ultracold magnets epitomizes the confluence of mathematics and physics, enriching our understanding of fundamental laws governing the universe. The emergence of this symmetry not only deepens our grasp of complex magnetic interactions but also propels a myriad of experimental and theoretical inquiries. As we uncover the rich tapestry woven by E8 symmetry and its ramifications, we stand poised at the frontier of a new era in physics—one where beautiful mathematical concepts translate into tangible discoveries, illuminating the essence of our universe and paving the way for groundbreaking advancements in technology.