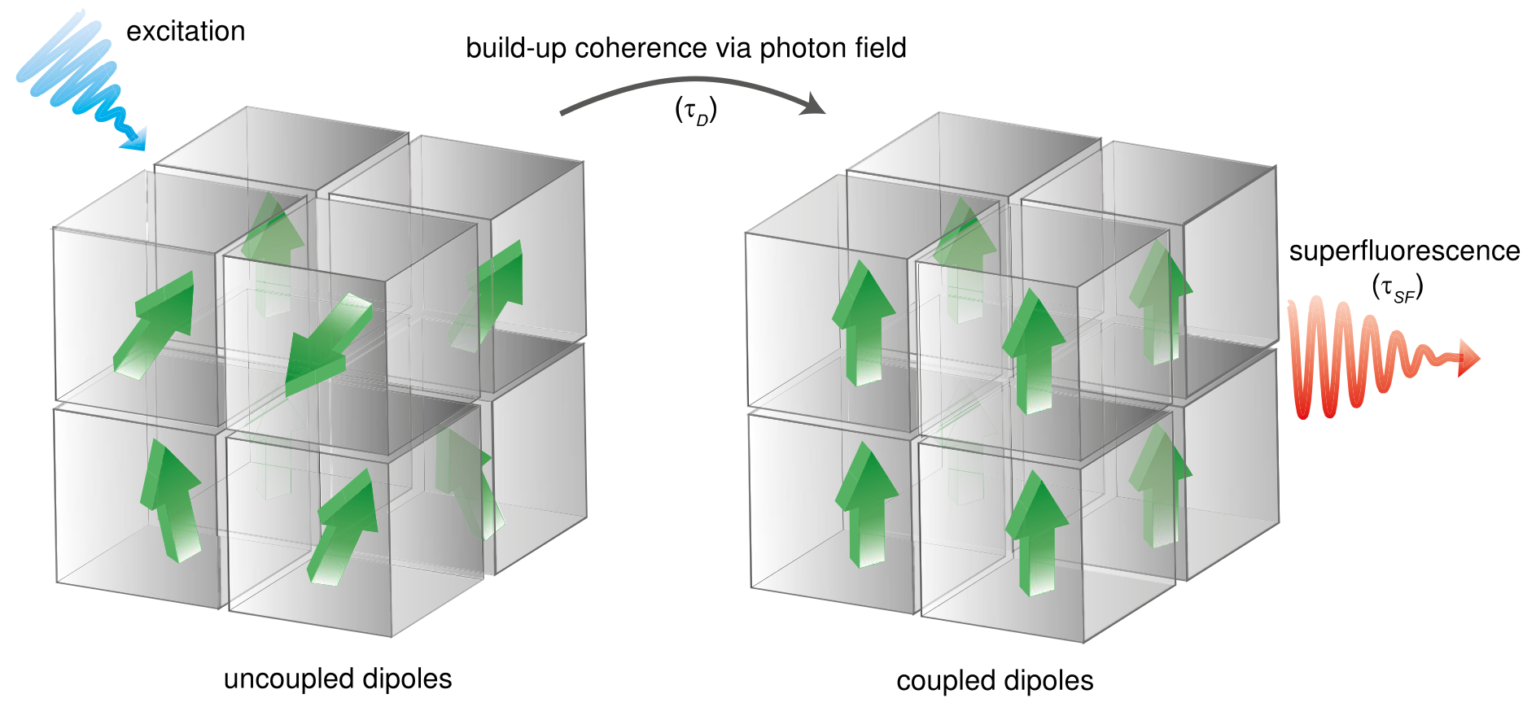
Research in condensed matter theory operates at the fascinating intersection of the abstract algebra of equations and the tangible realities of material phenomena. Much like the allegorical nature of alchemy—transforming base materials into gold—this field endeavors to elucidate the enigmatic behaviors of matter under varying conditions, exposing both microscopic interactions and emergent macroscopic phenomena. In this scholarly exposition, we will delve into the intricate methods, compelling metaphors, and the unique allure of performing research within condensed matter theory.
To embark upon this intellectual odyssey, one must first appreciate the multifaceted nature of condensed matter itself. At its core, condensed matter physics explores the states of matter that emerge from the assembly of vast numbers of atoms and molecules. Whether examining the crystalline lattices of solids or the chaotic dance of liquids, the quest is to decipher the fundamental interactions that govern these systems. This intricate tapestry of matter is akin to a symphony, where each atom plays a pivotal role, contributing to a harmonious or dissonant orchestration of physical properties.
Theoretical frameworks in condensed matter theory are primarily constructed around a set of mathematical formulations. Herein lies the challenge and beauty of the discipline: the ability to translate complex physical concepts into the language of mathematics. These formulations can often appear daunting, filled with tensors, integrals, and wave functions, evoking the image of a cryptic script waiting to be deciphered. However, each equation is a potential key, unlocking the secretive behaviors of materials—from superconductivity to quantum phase transitions.
One of the hallmarks of research in this field is the utilization of paradigms such as mean-field theory, renormalization group approaches, and quantum field theory. Each framework offers distinct insights, yet they share a common goal: to bridge the gap between the micro and macro worlds. Within the realm of mean-field theory, for instance, the interactions of particles can be simplified by averaging their effects, much like the way one might perceive the average temperature of a room rather than the individual oscillations of air molecules. This abstraction serves as a vital tool, allowing researchers to focus on overarching principles while simultaneously neglecting specific interactions that may complicate understanding.
Contrast this approach with the detailed richness afforded by renormalization group methods. This technique elegantly reflects the fractal nature of physical systems, where phenomena exhibit self-similarity across various scales. In this light, condensed matter research is reminiscent of peeling an onion—each layer of complexity reveals deeper insights into the underlying structure of matter. As one navigates these hierarchical layers, one can uncover universal properties that remain invariant despite the intricacies of specific systems.
The allure of conducting research in condensed matter theory beckons not only through its theoretical promises but through its profound implications on real-world applications. The insights garnered from this field resonate through technological innovations, influencing the development of materials such as superconductors, magnets, and semiconductors. Each breakthrough serves as a testament to the relevance of theoretical research, reinforcing the notion that equations are not merely abstract constructs but harbingers of tangible advancements in technology.
Moreover, the interplay between theory and experiment becomes a captivating dialogue, wherein theoretical predictions lead to experimental validation, and vice versa. This synergy between numerical simulation and laboratory investigation embodies the relationship between equations and reality. Just as an artist’s palette transforms mere colors into a vivid masterpiece, experimental results bring life to the theoretical frameworks that seek to explain them. This interplay fosters an iterative process, advancing both theoretical understanding and practical applications in tandem.
Within the condensed matter arena, the quest for new materials often resembles a modern-day treasure hunt. Researchers immerse themselves in the vast ocean of possibilities, sifting through various compositions and structures in pursuit of extraordinary properties. The search for topological insulators, for instance, unveils a previously uncharted territory ripe for exploitation; these materials hold the promise of revolutionizing quantum computing, where data flows with minimal resistance and astonishing efficiency. It is akin to navigating an uncharted archipelago of islands, each promising new discoveries and transformative impacts on society.
As researchers traverse this complex landscape, equipped with an arsenal of mathematical tools and experimental knowledge, they must grapple with the perennial challenge of uncertainty. Much like venturing into the depths of the ocean, where unpredictability reigns and new discoveries await, condensed matter theory is rife with enigmas and unanswered questions. Figuring prominently in this milieu are concepts such as quantum entanglement and emergent phenomena, which continually expand the boundaries of our comprehension.
Ultimately, the pursuit of research in condensed matter theory conjures an appealing dichotomy: one foot rooted firmly in the rigorous realm of mathematics, the other traversing the dynamic landscape of physical reality. It epitomizes the age-old quest of humanity to untangle the intricate threads of existence, to decipher the fundamental principles that govern the universe, and to infuse that understanding into our technological fabric. This duality epitomizes the notion that enduring knowledge is achieved only through the relentless interplay between equations and reality—a ceaseless journey characterized by inquiry, discovery, and profound connection to the very essence of nature itself.