The concept of fractional charge occupies a unique and intriguing position in the tapestry of theoretical physics. While electric charge is typically perceived in whole units, such as the elementary charge carried by electrons and protons, the possibility of fractional charge revolutionizes our understanding of fundamental particles and forces. This phenomenon arises intricately within the framework of quantum mechanics and condensed matter physics, especially as it relates to the fractional quantum Hall effect (FQHE) and other exotic states of matter.
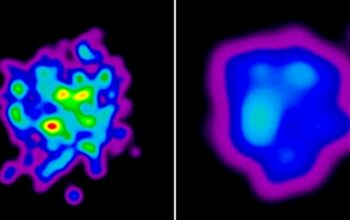
At the core of the fascination with fractional charge lies the empirical observation that certain systems exhibit quantized Hall conductance in fractions, specifically when subjected to strong magnetic fields at very low temperatures. This behavior emerges within two-dimensional electron gases, where interactions between electrons generate a strongly correlated state. Here, the electrons can effectively exhibit charges that are fractions of the elementary charge, a discovery rooted in theoretical predictions prior to its experimental realization in the 1980s.
The leading theoretical framework explaining fractional charge is provided by the concept of flux attachment. In the regime where strong magnetic fields are applied, electrons can combine with quantum flux quanta, effectively transforming to entities that behave like quasi-particles. These composite particles, which include “anyons,” display fractional statistics different from conventional bosons and fermions. That is, they exist in an intermediary state, causing a non-trivial braid when exchanged, leading to a manifesto of topological order.
Further elucidating the phenomenon of fractional charges requires an examination of the mathematical underpinnings governing particle interactions. The semi-classical approach to understanding electric charge leads to the realization that in specific dimensionalities, conventional definitions falter, yielding a requirement of a broader perspective influenced by topology and geometry. The presence of fractional charge suggests a compendium of physics that encompasses both quantum field theory and topological field theory.
The fractional quantum Hall effect serves as a paradigm to illustrate how condensed matter systems can provide insights into more foundational issues in physics. The observation that the Hall conductance can assume quantized values such as e²/h, e/3h, or e/5h, where e represents the elementary charge and h is Planck’s constant, not only substantiates the existence of fractional charge but posits the interconnectedness of quantum field theories with emergent behaviors in materials science.
This merging of concepts calls for an investigation into how fractional charge operates within the lattice structures of electrons. The integer quantum Hall effect thrives on a simplistic model of electrons confined in a two-dimensional plane, culminating in a quantization of Hall conductance under the domination of a magnetic field. However, scrambling the interactions through various means leads to the emergence of anyons and subsequent states exhibiting fractional charges. The non-trivial braiding statistics of anyons begs heuristic interpretation, inching toward a merging of particle physics and condensed matter phenomena that underscore the universality of certain critical attributes.
Furthermore, fractional charge is not an abstract notion confined solely to condensed matter systems. Theoretical constructs suggest potential implications in the study of higher-dimensional theories, which are emergent within string theory frameworks. Here, the brane-world scenarios bring forth a tantalizing aspect hinting at various forms of charge structure, and possibly hinting at novel interactions beyond the Standard Model.
As investigations into fractional charges continue to progress, numerous experimental techniques leverage advancements in technology to probe and manipulate the conditions where fractional charge phenomena manifest. Quantum dots, topological insulators, and artificial graphene are contemporary platforms where researchers endeavor to synthesize platforms conducive to fractional charges. By utilizing ultra-cold atoms or engineered quasi-1D and 2D systems, one can examine and validate the intricate behaviors anticipated by theoretical models. These explorations bridge understanding across disciplines, presenting a confluence of quantum mechanics, condensed matter, and confirming the interplay of fundamental principles.
As remarkable as fractional charge may seem, its implications stretch far beyond our present understanding of particle physics; it beckons a challenge to rethink fundamental constructs that govern our perception of charge and matter. The existence of fractional charges fosters inquiry into realms that not only question the nature of quantization but also evoke philosophical discourse on the underpinnings of reality itself. It demands a reconsideration of established paradigms and reflects the evolving nature of theoretical inquiry within physics.
In summary, fractional charge represents a compelling intersection of theoretical predictions and experimental realizations that can illuminate the subtleties of quantum mechanics and condensed matter physics. As a subject matter, it embodies a signal of the richness of physical phenomena awaiting discovery. Addressing both common observations and extraordinary cases, fractional charge serves as a powerful testament to the interconnectedness of diverse physical principles and the relentless quest to unveil the mysteries of our universe.