Mathematical models play a fundamental role across various disciplines, providing a scaffold on which complex phenomena can be analyzed and understood. These models serve as abstract representations of real-world systems, allowing scholars and practitioners to apply mathematical reasoning to predict behaviors, draw conclusions, and implement solutions. This article delineates the essence of mathematical models, elucidating their types, applications, and inherent significance in both theoretical and practical contexts.
Defining a Mathematical Model
A mathematical model is essentially a mathematical representation of a system or process. It utilizes mathematical language and concepts to describe the dynamics of systems, enabling the exploration of relationships between variables. At its core, a mathematical model encompasses a set of equations or functions that delineate the rules governing the system’s behavior. These representations may take various forms — from simple algebraic equations to complex differential equations — depending on the intricacies of the system being modeled.
Types of Mathematical Models
Mathematical models can be broadly categorized into several types, each serving specific analytical purposes:
- Deterministic Models: These models assert a precise relationship between variables; given the initial conditions, they yield a single, unambiguous outcome. A quintessential example is Newton’s laws of motion, where forces and accelerations are described mathematically. Such models are pivotal in physics and engineering, where predictability and precision are paramount.
- Stochastic Models: Contrarily, stochastic models incorporate randomness and uncertainty, mirroring the unpredictable nature of many real-world phenomena. They utilize probability distributions to account for the variability in outcomes. Applications of stochastic modeling are prolific in fields such as finance, where market uncertainties necessitate investment strategies that incorporate risk assessments.
- Static Models: These models analyze systems at a particular instance in time, ignoring temporal dynamics. They often serve as benchmarks or reference points for more complex analyses. Static equilibrium models, for instance, are fundamental in economics, providing insights into consumer behavior under assumed constant conditions.
- Dynamic Models: In contrast, dynamic models account for changes over time, incorporating differential equations that express how a system evolves. They are indispensable in fields such as biology, where population dynamics are affected by factors like birth rates and carrying capacity, which evolve over time.
- Linear vs. Nonlinear Models: Linear models maintain proportionality between variables, ensuring that changes in inputs lead to direct, proportional changes in outputs. Nonlinear models, however, exhibit more complex behaviors, such as exponential growth or chaotic systems, revealing intricate relationships often exhibited in real-life scenarios. Nonlinear dynamics are pivotal in meteorology and ecology, where small changes can yield disproportionately large effects.
Applications of Mathematical Models
The utility of mathematical models transcends disciplinary boundaries, manifesting in diverse fields like physics, biology, economics, and social sciences. Here are notable applications:
- Engineering: Engineers leverage mathematical modeling to simulate and optimize design processes. Finite element analysis, for instance, utilizes mathematical models to predict how structures respond to forces, facilitating the creation of safer buildings and infrastructure.
- Environmental Science: Climate models are a prominent example of mathematical modeling in environmental studies, analyzing the interplay between greenhouse gas emissions and climate change. These models enable policymakers to evaluate potential outcomes and make informed decisions regarding climate strategies.
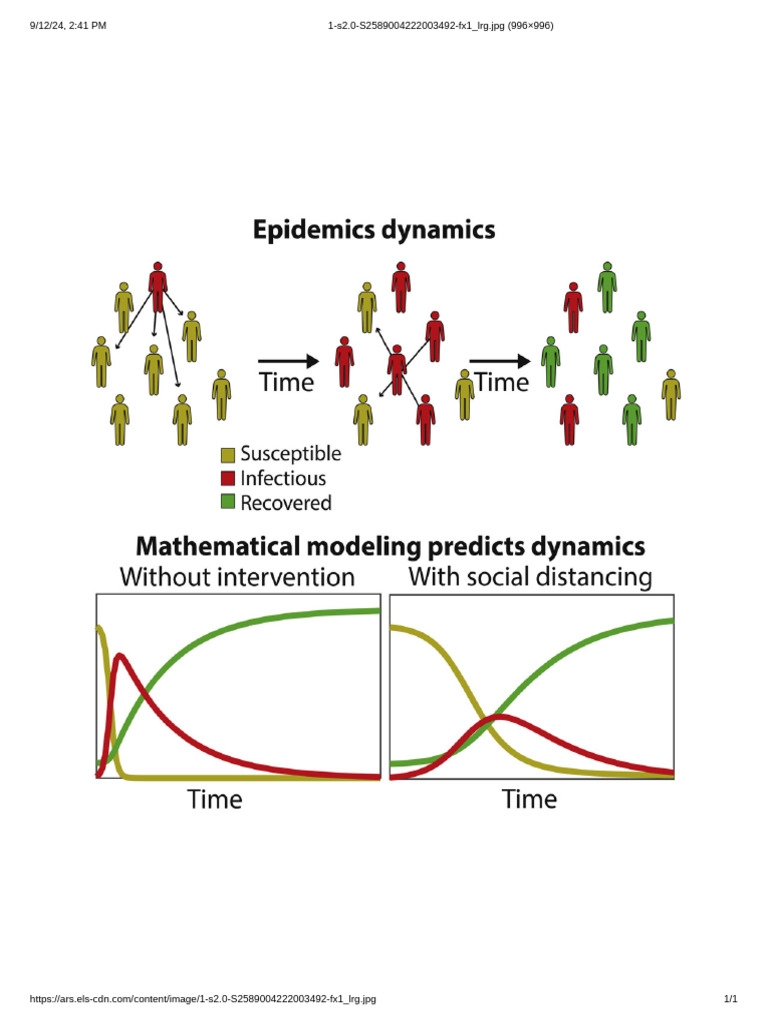
- Healthcare: In epidemiology, mathematical models are deployed to forecast the spread of diseases. The susceptible-infected-recovered (SIR) model exemplifies this, providing insights into how infectious diseases propagate through populations, thereby informing public health responses.
- Economics: Econometric models utilize mathematical frameworks to interpret economic data and forecast market trends. These models enable economists to analyze relationships between economic indicators and predict future economic conditions, guiding policy formulation.
The Process of Creating a Mathematical Model
The formulation of a mathematical model generally follows a systematic process. Initially, one must identify the problem and define the objectives clearly. Subsequent steps involve constructing the model by choosing appropriate variables and parameters, developing mathematical relationships, and deriving the relevant equations.
The model is then subjected to validation against empirical data to assess its accuracy and reliability. This calibration process is vital; a model that fails to predict real-world phenomena is rendered ineffective. After validation, sensitivity analyses are often conducted to explore how variations in parameters affect outcomes, further refining the model’s applicability.
Limitations of Mathematical Models
While mathematical models are powerful tools, they are not devoid of limitations. Assumptions underlying a model can simplify reality to a degree that renders predictions inaccurate or misleading. The choice of variables and the model’s structure can introduce biases that may obscure true relationships. Furthermore, unforeseen external factors may influence outcomes in ways that cannot be captured by the model, thereby introducing uncertainties.
Conclusion
Mathematical models are indispensable in the pursuit of understanding complex systems across diverse fields. Their ability to encapsulate relationships and predict behaviors facilitates informed decision-making, innovation, and the advancement of knowledge. As technological advancements continue to evolve, the refinement and enhancement of mathematical models will undoubtedly play a critical role in navigating the challenges and uncertainties of the modern world.