The Ising model, a simplistic yet profound framework in statistical mechanics, emerges as a cornerstone in the journey of understanding phase transitions and critical phenomena. This model, gleaned through the lens of a lattice of spins that can exist in one of two states—up or down—captures the essence of interactions at the microscopic level. It is a paradigm that reflects the dynamic complexities of physical systems, akin to a delicate ballet where each dancer’s movements influence her partners.
As one delves deeper into the realm of the Ising model, it becomes evident that its elegance lies not in its intricacy but in the depth of insights it provides. It is, poetically, the use of simple rules to navigate through the labyrinthine pathways of thermodynamic behavior. The model can be perceived as a stark canvas upon which the intricate tapestry of phenomena such as magnetism is painted, demonstrating how local interactions precipitate global behavior.
The foundational aspects of the Ising model center upon discrete variables and nearest-neighbor interactions, a simplification that yields substantial predictive power. In this model, each spin interacts with its immediate neighbors, leading to the emergence of order from disorder—a principle underlying many natural systems. The synchronous flipping of spins corresponds to the myriad of phases exhibited by resultant states, revealing an oscillating dance between chaos and coherence, much like a pendulum swaying with the rhythm of external influences.
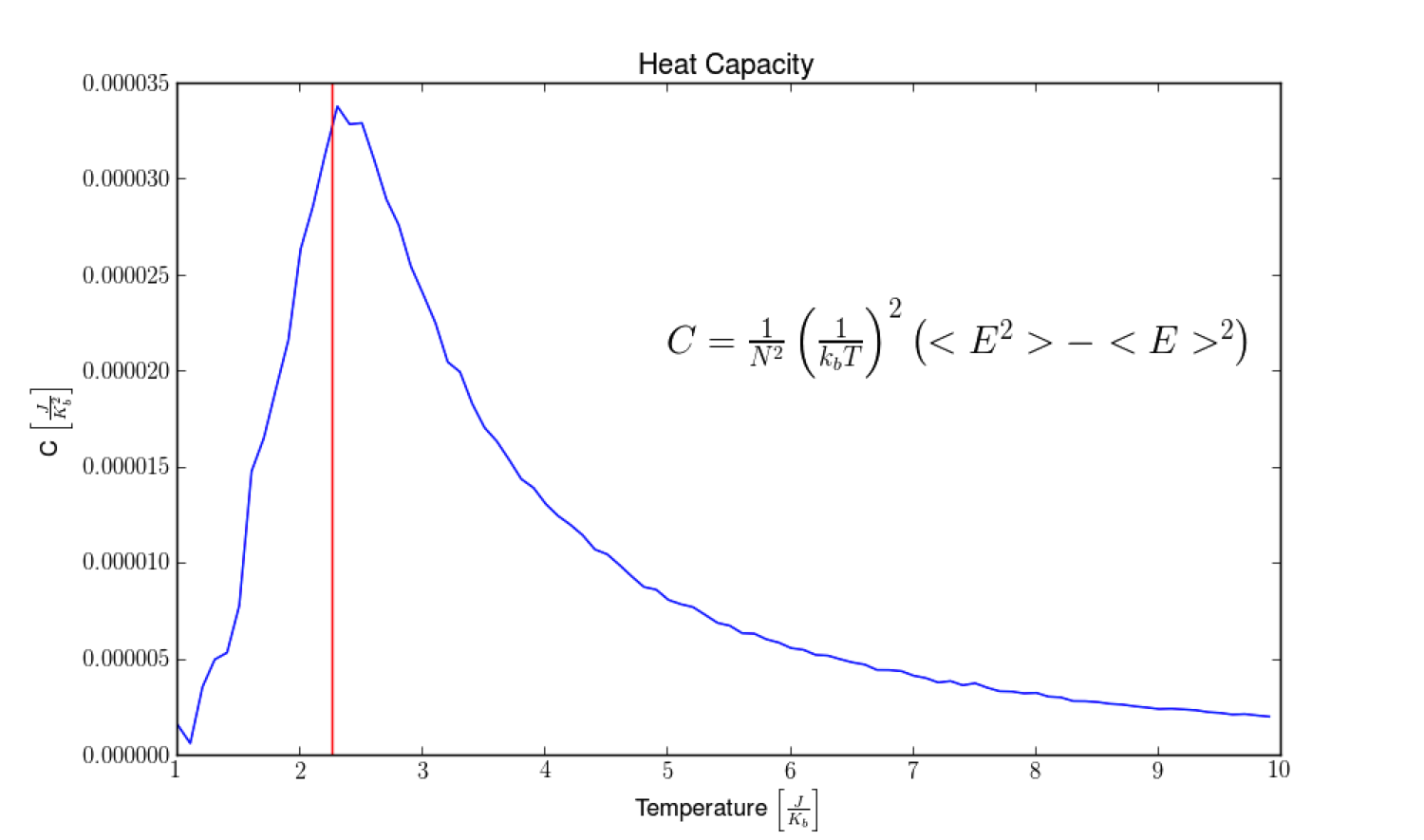
Historically, the model was conceived in 1925 by Ernst Ising while investigating ferromagnetism. Although initially formulated for one-dimensional lattices, subsequent research unveiled its potential when applied to two-dimensional and higher-dimensional constructs. The two-dimensional square lattice is particularly noteworthy, demonstrating a phase transition at a critical temperature, marked by a spontaneous magnetization occurring when temperature descends below a certain threshold. This pivotal phenomenon underscores the Ising model’s capability to explain not solely magnetic behavior but also diverse systems ranging from biological populations to social interactions.
At the heart of the Ising model is the Hamiltonian, which encapsulates the energy contributions deriving from spin orientations and interactions. The mathematical complexity of this expression belies its conceptual clarity; it is a function that assimilates the essence of competition between thermal agitation and interaction energies. This duality spirals into an exquisite portrayal of how microstates intricately inform macrostates, establishing a bridge between the quantum realm and classic thermodynamic behavior.
One of the most captivating aspects of the Ising model lies in its capacity to elicit critical phenomena, typified by phase transitions. As temperature approaches the critical point, the system exhibits a drastic response—a hallmark of phase change. The fluctuation of spins magnifies, and correlations extend across the system, akin to a ripple effect on a tranquil pond. This behavior transcends simplicity, revealing critical exponents and universal scaling laws that govern diverse systems; the Ising model is not merely a model of magnetization but a harbinger of universality in physics.
The exploration of the Ising model burgeons when extended to infinite lattices known as the thermodynamic limit. In this framework, concepts such as long-range order and spontaneous symmetry breaking materialize. The elegance of phase diagrams and critical points manifests as a visual representation of states, much like a cartographer delineating unknown territories of a vast landscape. Here, the language of phase diagrams becomes indispensable, portraying how varying conditions, such as temperature and external magnetic fields, influence the stability and phases of the system in an intricate dance of equilibrium and disequilibrium.
The interplay between computational advancements and the Ising model has birthed significant methodologies such as Monte Carlo simulations. Employing stochastic techniques to sample configuration space, these simulations unravel the intricate dance of spins over time, contributing to a vivid exploration of non-equilibrium phenomena. This confluence of computational power and theoretical refinement underscores how the Ising model withstands the vicissitudes of experimental scrutiny, revealing layers of complexity hidden beneath its ostensibly simplistic façade.
Moreover, the Ising model’s implications traverse beyond condensed matter physics, penetrating fields like network theory and complex systems. It serves as a paragon for understanding social dynamics, where spins represent individuals’ opinions or states in a sociopolitical context. Here, the interactions resonate with parallel narratives, where consensus emerges from initially disparate voices, echoing the phenomena of polarization and collective behavior. This metaphor, encompassing both the micro and macro realms, exemplifies how the Ising model provides a versatile framework for interpreting diverse phenomena across varied disciplines.
Despite its apparent simplicity, the Ising model continuously captivates the intellect of researchers. It manifests an enduring enigma, retaining its capacity to beget profound questions and rich dialogues in the discourse of physics. This model, encompassing the spirit of discovery and the quest for knowledge, reflects the very fabric of scientific inquiry—a perpetual dance between the known and the unknown, revealing that even the simplest systems can conceal richness and complexity that perplex and inspire. Thus, the Ising model stands as both a testament to and a puzzle in the landscape of modern physics.
In summation, the Ising model, with its elemental construction and profound implications, fosters a unique appreciation of the intricate realities underlying phase transitions. It operates as a bridge, connecting the meticulous laws of microscopic interactions to the breathtaking phenomena observable in macroscopic systems. As such, it continues to be a cherished fount of inspiration and a beacon guiding the enduring quest for understanding in the bosom of physical sciences.