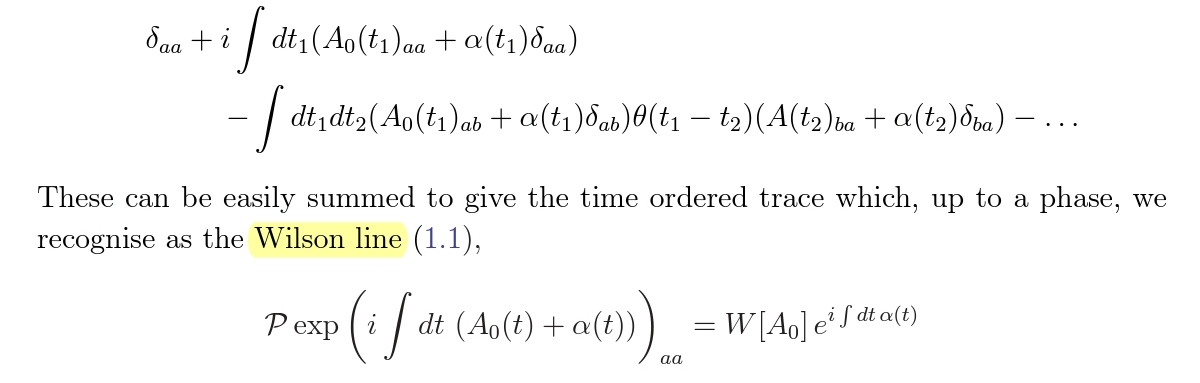The Wilson loop is traditionally conceived as a tool primarily within the realm of particle physics, particularly in the study of gauge theories and quantum chromodynamics (QCD). However, recent advancements in theoretical physics have illuminated the profound implications of the Wilson loop that extend beyond the confines of particle physics. This article delves into the burgeoning interdisciplinary applications of the Wilson loop, revealing its potential to transform our understanding of various physical phenomena.
Understanding the Wilson Loop
At its core, the Wilson loop represents a gauge-invariant quantity that encodes important information about gauge fields. Introduced by Kenneth Wilson in the early 1970s, it was conceived as a mathematical construct to explore the non-perturbative aspects of quantum field theory. Specifically, the Wilson loop is defined as a path integral over a closed loop in spacetime, integrating the gauge field along the trajectory. This elegant formulation facilitates the computation of important physical observables, including the area law behavior indicative of confinement in QCD.
A Historical Perspective
Initially, the significance of the Wilson loop was primarily recognized within high-energy particle physics. It facilitated a rigorous approach to understanding the strong force that binds quarks together within protons and neutrons. The treatment of the Wilson loop in lattice gauge theories underscored its utility in non-perturbative calculations, such as evaluating potential energy between quarks. The mathematical machinery developed for this purpose laid a solid foundation for future explorations across diverse domains.
Emerging Applications in Condensed Matter Physics
In recent years, the Wilson loop has transcended its original framework, permeating the field of condensed matter physics. Researchers have begun to exploit the Wilson loop to analyze topological phases of matter, most notably in systems exhibiting topological insulators and quantum Hall effects. Here, the Wilson loop serves as a powerful tool in identifying and characterizing topological invariants, which govern the emergence of protected edge states and bulk properties of these exotic materials.
Moreover, the presence of insulating phases and the intricate interplay between symmetry and topology can be effectively explored through the lens of the Wilson loop. Specifically, in the study of two-dimensional electron gases, the Wilson loop can yield insight into the emergence of fractional statistics and anyonic excitations. The capacity of the Wilson loop to encapsulate such nuanced topological information marks a pivotal expansion of its applicability beyond particle physics.
Applications in Quantum Gravity
Beyond condensed matter, the Wilson loop has found novel applications within the theoretical domain of quantum gravity. As researchers grapple with reconciling general relativity and quantum mechanics, the gravitational Wilson loop emerges as a promising avenue. It offers a framework to quantify the entanglement of spacetime geometry and quantum field interactions.
In the context of loop quantum gravity, the Wilson loop provides a quantization of areas and links between discrete spacetime structures. This intersection illustrates how the fabric of spacetime at a Planckian scale informs our understanding of gravity and quantum entanglement. The Wilson loop embodies a bridge uniting two paradigms previously thought disparate, fostering a deeper comprehension of the universe at its most fundamental level.
Topological QFT and the Wilson Loop
In the realm of topological quantum field theory (TQFT), the Wilson loop emerges as a critical building block for understanding anomalies and quantum states associated with knots and links. TQFT effectively utilizes the properties of the Wilson loop to construct invariants that are sensitive to the topology of the underlying manifold. This conceptual leap not only rekindles interest in classical knot theory but also intertwines it with cutting-edge physicists’ inquiries about quantum entanglement and invariant properties in high-dimensional spaces.
The intimate relationship between the Wilson loop and TQFT underscores the principle that a physical system’s behavior can be comprehensively described by its topology. The potential for extracting topological invariants from Wilson loops bears significance for quantum computing, where these invariants can inform efficient algorithms and fault-tolerant quantum gates.
Interdisciplinary Future of the Wilson Loop
The implications of the Wilson loop stretch far beyond the immediate realms of particle and condensed matter physics. This versatility heralds a transformative potential within fields such as cosmology, where the interactions between quantum fields and the early universe’s fabric can be elucidated. The interplay of quantum fluctuations and gravitational fields might be studied through generalized Wilson loops, providing insights into the quantum structure of spacetime itself.
Furthermore, emerging concepts such as quantum networks and information theory stand to benefit from the sophisticated structures instantiated by the Wilson loop. As theorists explore networks of quantum entanglement, the loop may furnish crucial insights into the organization and behavior of these networks, informing the design and implementation of next-generation quantum technologies.
Conclusion
The Wilson loop has indeed evolved from its original incarnation as a mere artifact of particle physics into a formidable tool with far-reaching applications across various branches of physics. Its newfound versatility prompts a significant shift in perspective, inviting researchers to reconsider established paradigms and explore uncharted interdisciplinary territories. As the boundaries between fields continue to blur, the promise of the Wilson loop serves as a beacon for innovative theories and experiments. The ongoing evolvement of its applications paves the way for exciting discoveries that could redefine our comprehension of nature and the underlying principles that govern it.