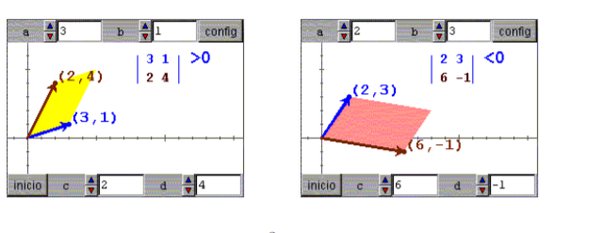
Las matrices jacobianas son herramientas matemáticas esencialmente útiles en múltiples ramas de la física. Estas matrices prestan un vital apoyo en el análisis de sistemas complejos y fenómenos que requieren el estudio de transformaciones y derivadas parciales. En este artículo, se exploran diversas aplicaciones de las matrices jacobianas en diferentes campos de la física, destacando su relevancia y adaptabilidad.
1. Mecánica Clásica y Dinámica de Sistemas
En la mecánica clásica, las matrices jacobianas son utilizadas para transformar coordenadas en el espacio y el tiempo. Consideremos un sistema de partículas donde las posiciones de las partículas están descritas en términos de coordenadas generales. La matriz jacobiana se constituye como la derivada de estas coordenadas generales con respecto a las coordenadas cartesias. Esto resulta esencial cuando se analizan sistemas en diferentes marcos de referencia, como el paso de un sistema inercial a uno no inercial, donde las fuerzas ficticias pueden complicar el análisis del movimiento.
Además, en la dinámica de sistemas, la matriz jacobiana se puede emplear en la formulación de las ecuaciones de movimiento, destacando la relación entre las velocidades y las fuerzas que actúan sobre el sistema. En este contexto, es posible determinar las fuerzas que deben ser aplicadas para mantener un sistema en equilibrio, además de facilitar la identificación de los modos normales de oscilación de estructuras complejas como puentes o edificios.
2. Termodinámica y Mecánica Estadística
En el ámbito de la termodinámica, las matrices jacobianas desempeñan un papel crucial en la formulación de las ecuaciones de estado. Estas ecuaciones permiten la descripción de relaciones entre diversas propiedades termodinámicas, como energía interna, entropía y volumen. Al utilizar matrices jacobianas, es posible calcular las derivadas parciales necesarias para determinar cómo cambia el estado de un sistema al variar ciertas coordenadas. Este enfoque es indispensable al estudiar sistemas fuera del equilibrio, donde las condiciones pueden cambiar drásticamente.
En la mecánica estadística, estas matrices pueden ayudar en el análisis de la relación entre variables macroscópicas y las propiedades microscópicas de los sistemas. El uso de la matriz jacobiana facilita el desarrollo del teorema de equipartición de la energía y proporciona los fundamentos necesarios para derivar distribuciones de probabilidad que rigen el comportamiento de sistemas grandes.
3. Electromagnetismo
La teoría electromagnética también se beneficia del uso de matrices jacobianas, particularmente en el estudio de campos eléctricos y magnéticos en diferentes coordenadas. Por ejemplo, al realizar la transformación de coordenadas desde un sistema cartesiano a uno cilíndrico o esférico, la matriz jacobiana juega un papel decisivo en la evaluacion de las relaciones entre los campos vectoriales y su geometría asociada.
Además, en el contexto de la teoría del potencial electromagnético, las matrices jacobianas son esenciales para el cálculo de corrientes y densidades de carga en sistemas complejos. Aplicaciones en circuitos eléctricos, antenas y otros dispositivos tecnológicos dependen de esta formalidad matemática para examinar la propagación de ondas electromagnéticas.
4. Relatividad y Cosmología
Las matrices jacobianas también se encuentran en el ámbito de la relatividad, donde se utilizan para formular transformaciones entre distintos sistemas de referencia que se mueven a velocidades relativistas. En este sentido, se convierten en herramientas esenciales para la formulación de las ecuaciones de movimiento de partículas en el espacio-tiempo curvado.
Asimismo, en cosmología, las matrices jacobianas están presentes en el análisis de la expansión del universo y el estudio de la geometría del espacio-tiempo. El uso de estas matrices permite describir cómo la curvatura del espacio-tiempo afecta la trayectoria de la luz y la distribución de galaxias, lo que es fundamental para comprender fenómenos como el desplazamiento al rojo y la formación de estructuras cósmicas.
5. Óptica y Acústica
En el campo de la óptica, las matrices jacobianas se utilizan para describir la propagación de ondas luminosas a través de diferentes medios. Las transformaciones que describen la variación de la amplitud y la fase de las ondas pueden ser representadas mediante estas matrices, facilitando el análisis de fenómenos como la difracción y la interferencia.
Del mismo modo, en acústica, las matrices jacobianas son pertinentes para describir la propagación de ondas sonoras en diferentes medios. Al modelar el comportamiento de estas ondas en entornos complejos, como en gabinetes de sonido o en la acústica arquitectónica, se puede establecer una relación clara entre las características del medio y el comportamiento de las ondas acústicas.
6. Conclusiones
Las matrices jacobianas son fundamentales para el desarrollo de numerosas teorías y aplicaciones en física. Desde la mecánica clásica hasta la relatividad y más allá, su versatilidad y capacidad para describir relaciones complejas son invaluables. No solo facilitan el estudio y la comprensión de sistemas físicos en diversas condiciones, sino que también sostienen la construcción matemática que subyace a la física moderna. A medida que la investigación continúa avanzando, es probable que surjan nuevas aplicaciones y técnicas que aprovechen aún más el potencial de las matrices jacobianas en la búsqueda de una comprensión más profunda de los fenómenos físicos que nos rodean.