Imagine a majestic labyrinth, its walls intricately woven with threads of prime numbers. Within this splendid maze, the secret to unlocking the treasures of the digital era lies concealed, waiting for an astute mind to wield a key capable of untangling its complexities. Enter Shor’s algorithm, a computational tour de force that has dramatically transformed the landscape of cryptography and quantum computing.
At its core, Shor’s algorithm is an ingenious procedure designed to factor large integers efficiently—a task that classical algorithms struggle to accomplish in a feasible time frame as the size of the integers increases. The significance of this feat cannot be overstated; it challenges the very foundation of cryptographic systems that depend on the assumption that factoring large composite numbers is computationally insurmountable. To fully appreciate the elegance of Shor’s algorithm, one must embark on an exploration of its foundations and implications.
To understand this groundbreaking algorithm, it is pivotal to delve into the realm of number theory, where prime numbers reign supreme as the building blocks of arithmetic. When two prime numbers are multiplied, they yield a composite number, yet the reverse operation—decomposing a composite number into its prime factors—poses a formidable challenge for classical computation. This is akin to being trapped within the confines of the labyrinth, where the exit is obscured, and the paths are labyrinthine in nature.
In the classical computing paradigm, algorithms such as those developed by the likes of the number field sieve may succeed in factoring integers, but their time complexity burgeons exponentially with the size of the integers involved. Consequently, the practicality of such algorithms diminishes substantially as they scale. In stark contrast, Shor’s algorithm presents a quantum approach that exponentially accelerates the factoring process, leveraging the peculiar properties of quantum mechanics such as superposition and entanglement.
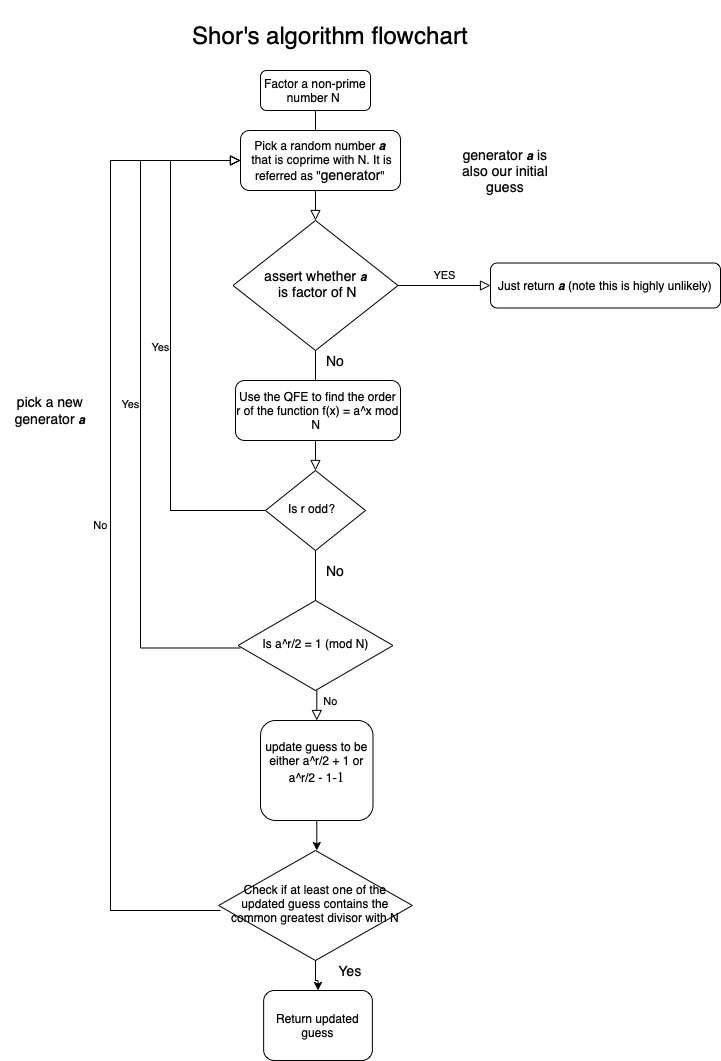
Shor’s algorithm operates through two fundamental phases: the quantum phase and the classical phase. The quantum phase relies on a pivotal component known as quantum Fourier transform (QFT), a mathematical operation that serves as the backbone of the algorithm’s efficiency. By initiating a series of quantum states—akin to a symphony of qubits dancing in harmonious synchrony—Shor’s algorithm is able to exploit the interference of probability amplitudes, thereby revealing the hidden periodicity inherent in the numbers involved.
The classical phase, on the other hand, engages traditional computational methods to extract the factors from the information gleaned during the quantum computations. This duality in operation, one foot in the realms of quantum mechanics and the other in classical computing, lends Shor’s algorithm its unique appeal: it harnesses the advantages of both worlds. Together, these two phases culminate in a dramatic reduction of the time complexity associated with integer factorization, slashing it from exponential time (as seen in classical algorithms) to polynomial time.
Yet, what makes Shor’s algorithm genuinely remarkable is not merely its ability to factor integers efficiently, but the profound implications it carries for the field of cryptography. Currently, many encryption protocols rely on the difficulty of factoring large numbers as their security basis, forming a robust shield against potential threats. However, the advent of an efficient quantum algorithm such as Shor’s incites a profound sense of vulnerability within these cryptographic frameworks, stimulating an urgent quest to devise quantum-resistant alternatives.
This conundrum has sparked a renaissance in cryptographic research, often described as post-quantum cryptography, where the focus has shifted to developing algorithms resilient against quantum attacks. This nascent field showcases the adaptability of computer scientists and mathematicians who are striving to envision and implement security systems capable of withstanding the advances of quantum computing. In this manner, Shor’s algorithm has catalyzed a paradigm shift not just within the bounds of computation but also throughout the intricate ecosystem of digital security.
Furthermore, the potential applications of Shor’s algorithm extend beyond the confines of number theory and cryptography. In a broader context, the algorithm epitomizes the possibilities that quantum computing holds for various scientific fields, from materials science to molecular biology. The ability of quantum computers to unravel complex problems efficiently could lead to advancements that were previously deemed impractical or unattainable using classical mechanisms.
In summation, Shor’s algorithm is akin to a key, unlocking the cryptographic labyrinth that safeguards our digital lives. Its dual-phase structure reflects the symbiotic relationship between quantum mechanics and classical computation, a dance of sorts that ultimately reveals profound truths about the nature of numbers and encryption. As we stand on the precipice of a quantum revolution, the implications of Shor’s algorithm will ripple through the fabric of technology and security, urging us to rethink our assumptions and innovate in a landscape where quantum and classical coexist.
To navigate this new reality, one must embrace the intricacies of quantum mechanics and its marriage to computational theory, recognizing that the elements of thought previously considered impenetrable are now within our grasp. Shor’s algorithm serves as a testament to human ingenuity and the relentless pursuit of knowledge, guiding us towards uncharted territories of computational prowess and offering glimpses into realms where problems that once seemed insurmountable can finally sway to the rhythm of quantum computation.