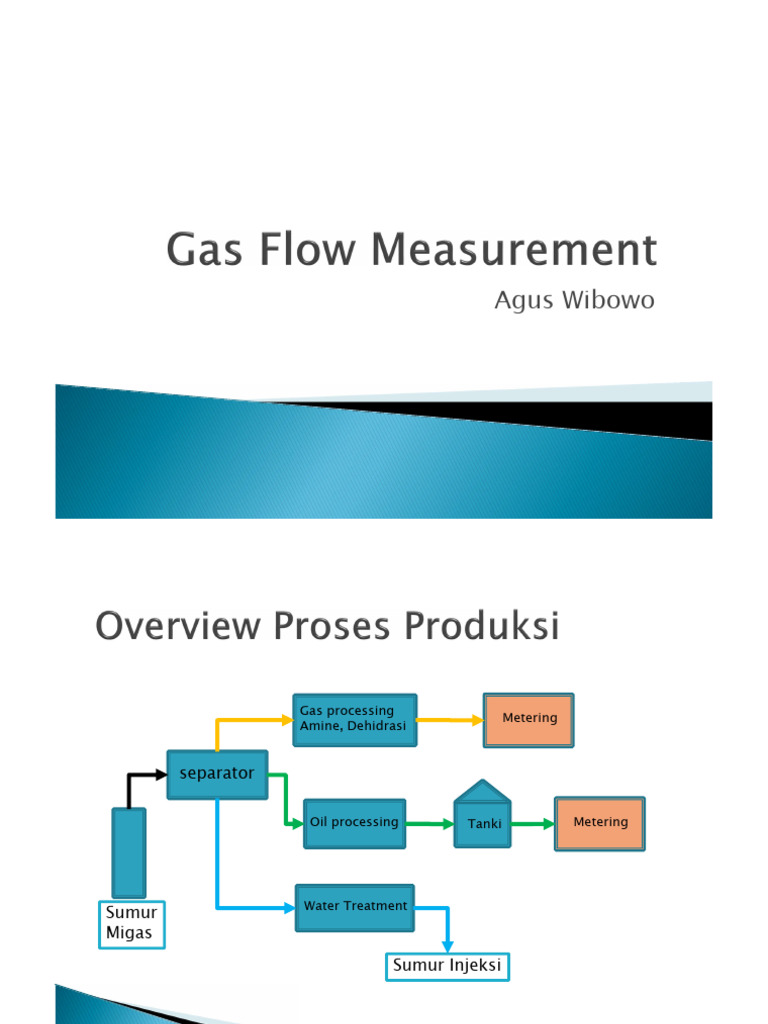
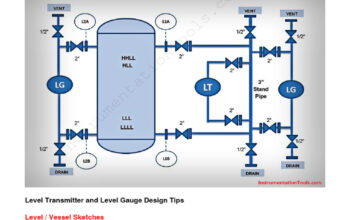
Measuring the flow rate of gas without resorting to traditional flow meters can seem like navigating a labyrinth of scientific inquiry, yet it is both an intriguing and indispensable endeavor. Various methodologies exist that utilize fundamental principles of physics and chemistry, offering innovative solutions for engineers and researchers alike. This discourse delves into several alternatives, each poised to facilitate a nuanced understanding of gas flow measurement, while inviting curiosity towards unconventional techniques.
To begin, it is essential to grasp the foundational concepts associated with gas behavior under varying conditions. Implementing the principles of fluid dynamics allows us to extrapolate flow rate measurements even in the absence of a conventional flow meter. One prominent method is the use of the orifice equation, which correlates the pressure differential across an orifice plate to the volumetric flow rate. By establishing precise measurements of pressure before and after gas traverses the orifice, one can apply Bernoulli’s principle to glean substantial insights into the flow behavior. This method requires careful calibration and consideration of fluid properties, including density and viscosity, particularly at varied temperatures.
Another innovative technique involves employing a Pitot tube, which, while technically a form of flow measurement device, can be adjusted in ways that sidestep conventional usage. The Pitot tube operates by comparing static and dynamic pressure, providing an alternative perspective on gas flow velocity. Although it is often associated with liquids, its applications in gaseous environments extend to aviation and other fields. By analyzing the velocity of a gas stream and applying the continuity equation, one can indirectly determine the flow rate, offering a fascinating intersection of theory and practical application.
For those who prefer a more empirical approach, the use of the gas discharge equation can yield fruitful results. This equation relates the mass flow rate of a gas to its physical properties and the conditions surrounding it. Specifically, if one knows the area of the outlet and the pressure differential, along with the temperature and molecular weight of the gas, it is feasible to ascertain flow rates without direct measurement tools. This technique represents an engaging challenge for students and professionals alike, combining theoretical knowledge with practical application.
Thermal mass flow measurement also proffers an interesting alternative to traditional methods. This technique leverages the principle of heat transfer, where a known amount of heat is imparted to a gas stream and, by measuring the resulting temperature change, one can infer the mass flow rate. The implementation of this method often requires specialized sensors; however, it provides an opportunity to explore the intricate relationship between thermal conductivity and gas properties, encapsulating curiosity-driven inquiry at its best.
Adopting the hydrostatic method facilitates yet another viable option. This approach is predicated on the variation in height of a gas column within an open container. By measuring the height difference, one can calculate the flow rate using the hydrostatic pressure equation. This method is particularly useful in laboratory settings and small-scale applications, where precision is crucial, and environmental variables are controlled. By emphasizing the significance of atmospheric pressure and density variations, this process highlights the broader implications of thermodynamics in fluid flow measurement.
Beneath this elaborate tapestry of methodologies lies the intriguing subject of computational fluid dynamics (CFD). Although decidedly more complex, CFD employs numerical simulation techniques to solve and analyze fluid flow behavior. Using sophisticated algorithms and models, practitioners can visualize and predict flow patterns, aiding in the assessment of gas flow rates. This approach demands a robust understanding of mathematical modeling, yet it opens the door to high-precision outcomes that can enhance design and operational efficacy in various fields.
Moreover, an intriguing perspective on gas flow measurement emerges through the integration of modern technologies. The advent of sensor technologies, such as ultrasonic and laser Doppler anemometry, allows for non-invasive measurements of gas velocity. While these devices can be costly and sophisticated, they exemplify the convergence of physics and engineering, paving the way for innovative applications in industrial processes, environmental monitoring, and aerospace engineering.
It is also worth noting how utilizing established gas laws, such as Boyle’s Law or Charles’s Law, can facilitate a deeper understanding of gas behavior under pressure and temperature variations. By performing controlled experiments, researchers can derive empirical data and correlate it to theoretical predictions, yielding a holistic view of gas flow dynamics. This empirical approach not only fuels curiosity but also underscores the scientific method’s role in enhancing our understanding of natural phenomena.
As one delves deeper into the realm of gas flow rate measurement without conventional flow meters, the convergence of theory, experimentation, and technology presents a rich tapestry of possibilities. It instills a profound curiosity about the ways in which we can harness physics to glean insights from the world around us. By embracing innovative methodologies, practitioners not only advance their technical skills but also contribute to the ever-evolving landscape of scientific inquiry, prompting a paradigm shift in how we perceive and engage with gas flow measurement.