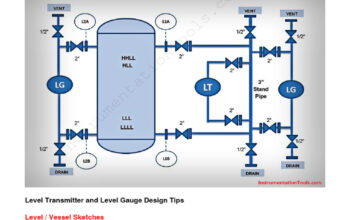
Electrical measurements form the bedrock of understanding the fundamental principles governing electrical phenomena. The allure of interpreting these measurements lies not only in their utility in practical applications but also in their capacity to unveil the intricate relationships between various electrical parameters. To navigate the complexities of electrical measurements, one must adopt a systematic approach that encompasses various types of measurements, techniques of interpretation, and the underlying principles that govern these phenomena.
Firstly, an appreciation of the different categories of electrical measurements is essential. Primarily, electrical measurements can be classified into three broad types: voltage, current, and resistance measurements. Voltage, measured in volts, represents the electric potential difference between two points. Current, quantified in amperes, reflects the flow of electric charge through a conductor. Resistance, expressed in ohms, measures the opposition to the flow of electric current. Each of these parameters provides critical insights into the behavior of electrical circuits.
When measuring voltage, one must consider the configuration of the measurement circuit. A voltmeter, ideally connected in parallel with the component under observation, allows for an accurate assessment of voltage drops. The technique of utilizing proper meter connection cannot be overemphasized, as improper connections may yield erroneous or misleading readings. For instance, if a voltmeter is connected in series with a load, the resultant voltage reading will be significantly affected, leading to potential misinterpretations about the circuit’s performance.
Current measurement requires the strategic use of an ammeter, which must be connected in series with the circuit element. A critical aspect of current measurement is understanding the impact of internal resistance of the ammeter on the overall circuit. An ammeter with high internal resistance can alter the current flow it is designed to measure, thereby distorting the data significantly. Hence, selecting the appropriate measuring instrument with a minimal disturbance to the circuit’s functionality is paramount.
Resistance, on the other hand, can be measured using an ohmmeter. When interpreting resistance measurements, one must be cognizant of the factors such as temperature, material properties, and physical dimensions of the conductor. The resistance of materials is directly proportional to their length and inversely related to their cross-sectional area. This relationship is encapsulated in the formula R = ρ(L/A), where R represents resistance, ρ is the resistivity of the material, L is the length, and A is the cross-sectional area. It is essential to factor in these parameters when drawing conclusions from resistance measurements.
Beyond the simplistic gathering of data lies the art of interpretation. A common observation among those engaged in electrical measurements is the propensity to overlook the contextual underpinnings of their data. Data points should not merely exist in isolation; rather, they are tangible manifestations of physical laws at play. Such laws, including Ohm’s law, Kirchhoff’s voltage law, and Kirchhoff’s current law, provide a theoretical framework for making sense of the measurements.
Ohm’s law, for instance, postulates a direct proportionality between voltage and current for a given resistor—articulated mathematically as V = IR. This fundamental relationship is not only central to electronics but also serves as the backbone of numerous circuit analysis techniques. By employing Ohm’s law, one may identify anomalies in measurements that could indicate underlying issues within the circuit, such as short circuits or open connections.
Moreover, the application of Kirchhoff’s laws extends the realm of interpretation further. Kirchhoff’s voltage law asserts that the total voltage around a closed loop must equate to zero. This principle elucidates the necessity of considering all voltage drops and rises within the circuit, allowing for a holistic view of electrical behavior. When discrepancies arise in the sum of voltages, it prompts a deeper investigation, potentially exposing defective components or unforeseen circuit conditions.
In addition to employing established laws, the significance of measurement uncertainty cannot be understated. Each measurement inherently carries a degree of uncertainty, influenced by factors such as instrument accuracy, environmental conditions, and measurement techniques. Understanding this uncertainty allows practitioners to evaluate the reliability of their results critically. Statistical analysis may sometimes be necessary to discern true trends from oscillations caused by external variances or instrument limitations.
Furthermore, advancements in technology, such as digital multimeters and oscilloscopes, have augmented the precision and ease of electrical measurements. Digital devices often come equipped with features that automatically calculate values, provide graphical representations, and facilitate data storage. However, a prudent professional must remain cognizant of the fact that technological reliance should never eclipse fundamental knowledge. The ability to understand and interpret the underlying principles remains paramount, particularly in troubleshooting complex electrical systems.
In conclusion, interpreting electrical measurements involves more than merely taking readings. It requires a comprehensive understanding of the theoretical underpinnings, meticulous attention to methodological precision, and an appreciation for the broader context of the measurements. As one delves into the art and science of electrical measurements, the rewards extend beyond mere data collection; they foster a profound encounter with the elegant dynamics of the electrical universe. By embracing this multifaceted approach, one may unlock the true potential of electrical measurements and their pivotal role in both academic inquiry and practical application.