Quantum computing, a transformative paradigm in computational theory and practice, has spurred considerable inquiry into its fundamental nature. At the heart of this exploration lies a provocative query: Is quantum computing merely an analog form of computation? This question not only invites scrutiny of the core principles of quantum mechanics but also challenges long-standing assumptions about computation itself. Let us delve into the intricacies of quantum computing to elucidate its distinctiveness and the complexities surrounding its classification.
To begin, we must establish a baseline understanding of what is meant by analog computing. Analog computers represent data through continuous physical phenomena, such as electrical voltage or mechanical motion. In contrast, digital computers use discrete binary representations to perform calculations. The distinction between these two modalities becomes crucial as we consider the mechanics of quantum computing, which operates on the principles of quantum mechanics, transcending classical delineations.
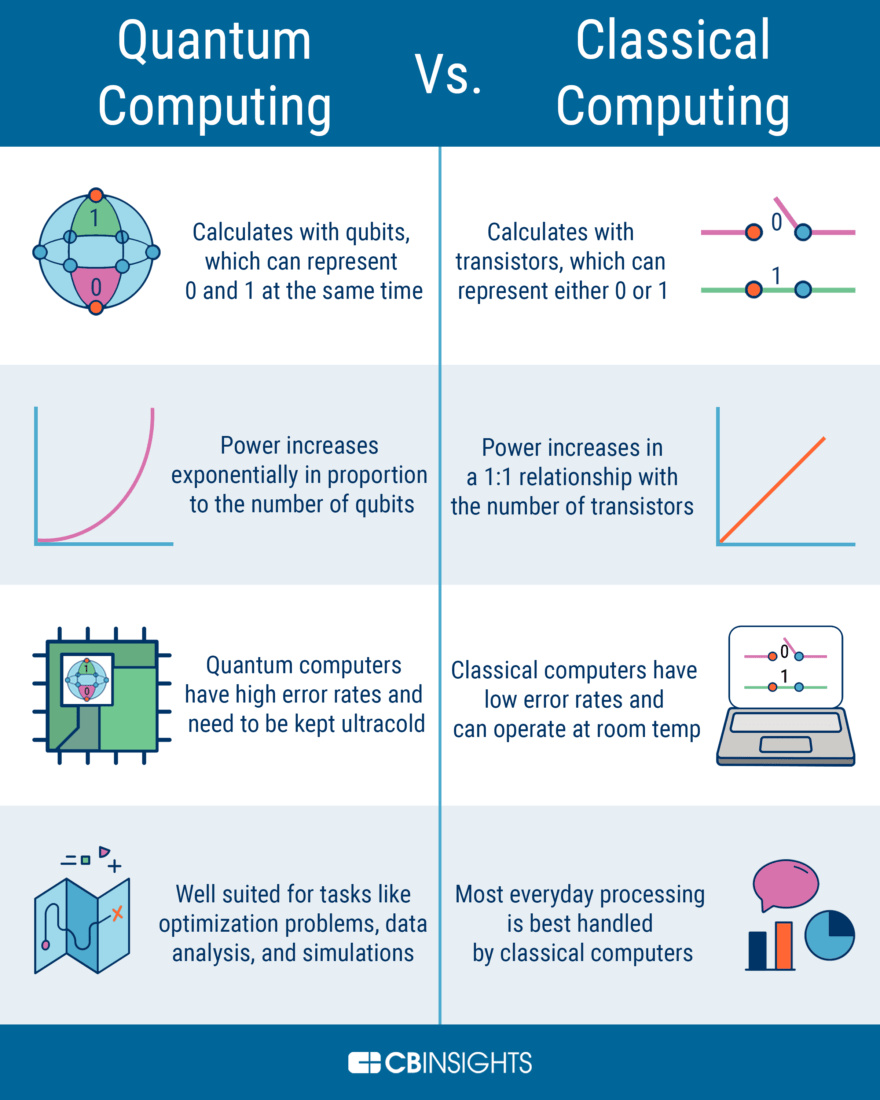
In quantum computing, information is processed using quantum bits, or qubits. Unlike classical bits, which can exist in one of two states (0 or 1), qubits possess a fascinating capability known as superposition. This allows them to simultaneously represent multiple states, a mathematical abstraction that introduces a degree of complexity not found in conventional analog or digital systems. Herein lies the first kernel of differentiation: while analog computers approximate real-world phenomena, quantum computing employs quantum states to exploit the probabilistic nature of quantum mechanics for processing information.
Consider the implications of superposition. When a qubit is in a state of superposition, it can perform computations in parallel, potentially addressing an exponential number of possibilities concurrently. This phenomenon leads us to query whether quantum computing’s ability to handle vast datasets is merely an enhancement of analog techniques or a fundamental advancement that cannot be reduced to classical analog or digital frameworks.
Moreover, entanglement occurs when qubits become interdependent, allowing changes to the state of one qubit to instantaneously affect the state of another, regardless of distance. This non-local correlation introduces a layer of connectivity that analog systems cannot replicate. In this light, one might argue that the very framework of quantum computation is predicated on a fundamentally different understanding of information and interaction compared to analog computing.
The comparison of quantum and analog systems extends beyond mere mechanics into the realm of application. Analog computers excel in specific tasks, particularly those involving differential equations, signal processing, and simulation of dynamic systems. They provide insights into continuous data streams and have been employed effectively in engineering and scientific modeling. However, as we grapple with complex problems, such as factorizing large integers (a central challenge in cryptography), quantum computing emerges as a formidable contender, promising computational efficiency that far exceeds its analog counterparts.
Nevertheless, one must not hastily dismiss the merit of analog computing as merely archaic. Modern technologies have rekindled interest in analog approaches, as evidenced by advancements in neuromorphic computing and mixed-signal processors. These developments emphasize the potential of hybrid systems that fuse the benefits of analog and digital technologies, highlighting the utility of computing paradigms beyond traditional definitions. But does this evolution strengthen the notion that quantum computing is simply an innovative branch of analog science?
As we ponder further, we must consider the implications of decoherence, a significant challenge faced by quantum systems. Decoherence refers to the loss of quantum coherence, whereby a qubit transitions from a superposition to a classical state upon interaction with the environment. It serves as a critical reminder that while quantum systems hold promise, they are exceedingly delicate and susceptible to external disturbances. This precariousness stands in stark contrast to the robustness typically associated with analog computing, which can perform within a broader scope of environmental variability without catastrophic failure.
To complicate the issue further, there are philosophical dimensions to explore. What constitutes computation in a quantum realm? Are we to redefine computation as a probabilistic mechanism, influenced by the tenets of quantum theory? These inquiries challenge existing definitions and prompt a reconsideration of how computation is conventionally approached. Hence, the analog nature of quantum computing, though alluring, may be a mischaracterization that oversimplifies a richly textured exposition of computation itself.
Another angle from which to interrogate this issue involves quantum algorithms—specific procedures designed to harness the inherent characteristics of quantum computing. Prominent examples, such as Shor’s algorithm for factoring integers and Grover’s algorithm for unsorted database searching, underscore the unique capabilities that quantum computation brings to bear on problem-solving, diverging sharply from analog computation methodologies. If quantum algorithms embody attributes that cannot be reconciled with the analog paradigm, does it render the analogy inherently flawed?
In conclusion, while it is tempting to conflate quantum computing with analog computations due to their shared goal of processing information, such a comparison may obscure the profound distinctions that define each modality. Quantum computing represents not merely an innovative advancement but a paradigm shift that extends our understanding of computation. Exploring the delicate interplay between superposition, entanglement, and decoherence amplifies the complexity of the quantum realm, inviting ongoing inquiry. As we stand at the frontier of this burgeoning field, it is imperative to consider the broader implications and potential challenges that arise from attempting to transcend traditional classifications of computation. Is quantum computing just analog? The answer remains tantalizingly elusive and indeed, may shape the future of computational thought for generations to come.