Quantum computing, a field that beckons a paradigm shift in classical computational frameworks, is fundamentally concerned with the manipulation of qubits. Unlike classical bits, which inhabit a binary realm of 0s and 1s, qubits exist in a superposition of states, manifesting a rich tapestry of physical representations that embody their unique characteristics. Understanding how qubits are physically represented not only illuminates the underlying principles of quantum mechanics but also underscores the transformative potential this technology holds for diverse fields.
At the core of the quantum mechanical framework lies the concept of superposition. A qubit can be represented as a point on the surface of a Bloch sphere, a geometrical representation that encapsulates all possible states of the qubit. The north pole represents the classical state |0⟩, while the south pole represents |1⟩. Any point on the surface indicates a superposition state, where the qubit may exist in various probabilities of being |0⟩ or |1⟩. The spherical symmetry facilitates visualization of the delicate interplay between the two states, rendering the qubit’s behavior both intuitive and enigmatic.
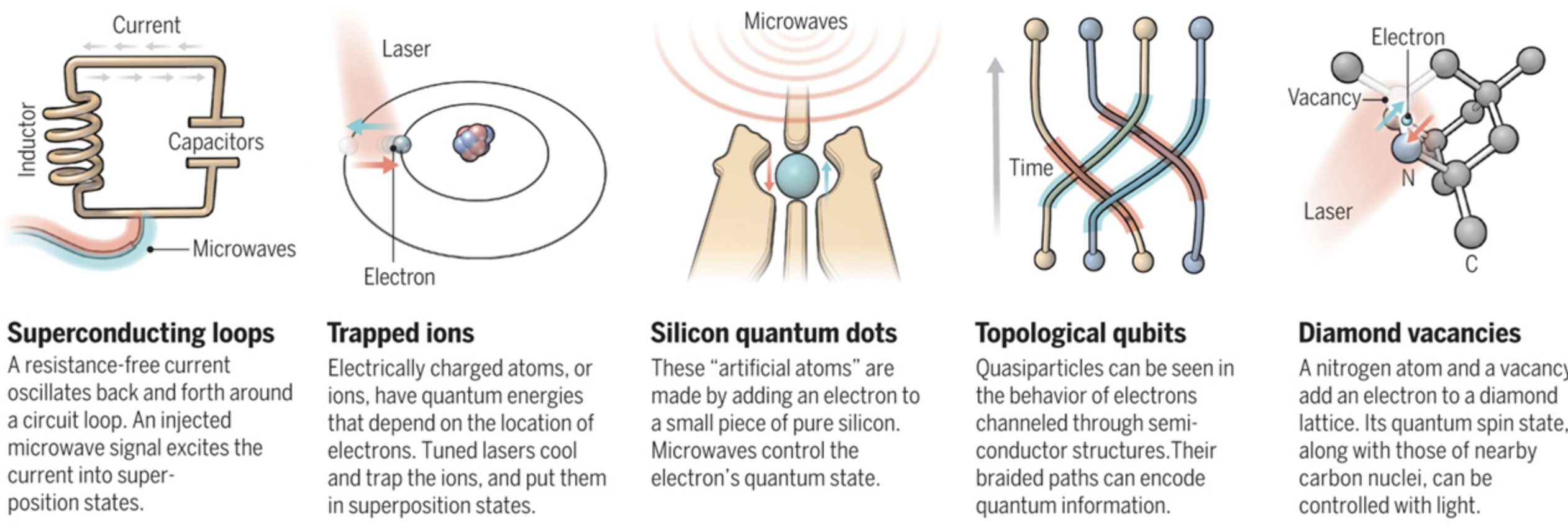
Several physical systems have been devised to implement qubits, each with its own merits and idiosyncrasies. One of the most prominent representations of qubits comes from superconducting circuits. Here, Josephson junctions are employed to create non-linear inductive elements that can oscillate, transitioning between distinct energy levels. In this scenario, qubits are manipulated via microwave pulses that coax them into desired superpositions. This physical representation has garnered significant attention owing to its scalability and the ability to fabricate numerous qubits on a single chip, thereby holding promise for large-scale quantum computation.
Optical qubits present another avenue of exploration, leveraging the quantum states of photons. A photon’s polarization can serve as a qubit, utilizing polarization states such as horizontal and vertical or circular polarization states—left-handed and right-handed—as the basis states. The advantage of optical qubits lies in their inherent resilience to decoherence, attributed to the robustness of light against environmental disturbances. Moreover, the ability to create entangled photon pairs via spontaneous parametric down-conversion provides remarkable opportunities for quantum communication and cryptography systems.
The realm of trapped ions exemplifies yet another physical representation of qubits. Here, individual ions are confined using electromagnetic fields, and qubit states are encoded in their electronic configurations. Coherent control over ion states is achieved through laser pulses that manipulate the ions’ transitions. Trapped ions exhibit extremely long coherence times, making them highly attractive for quantum computation. The precise control and measurement capabilities inherent in this approach allow for implementations of complex quantum algorithms, inspiring advancements in the field.
Quantum dots, semiconductor nanoparticles, constitute another promising avenue for realizing qubits. In these nanoscale structures, confining electrons leads to discrete energy levels, much like atom behavior. Manipulating the spin of these electrons allows for the encoding of qubit states, leveraging the electron’s intrinsic angular momentum. While still in the developmental phase, research into quantum dots is pivotal for developing robust quantum networks and integrated circuits, potentially leading to revolutionary advancements in information processing.
A less commonly discussed but intriguing physical representation of qubits is the use of nuclear magnetic resonance (NMR). NMR quantum computing employs the magnetic resonance properties of atomic nuclei, where the nuclear spin states correspond to the qubit states. Though NMR techniques are limited in scalability due to the complexity of required control and measurement apparatus, they serve as an enlightening framework for exploring quantum algorithms and fundamental concepts in quantum theory.
As diverse as these representations are, each physical realization of a qubit wrestles with the challenges posed by decoherence. In the quantum realm, interaction with the environment can collapse superpositions into definite states, undermining the delicate computations. Therefore, mitigating decoherence emerges as a quintessential goal within quantum technology. Initiatives such as topological qubits—the theoretical embodiment of qubits formed by the braiding of non-abelian anyons—seek to enhance resilience against such perturbations, potentially enabling fault-tolerant quantum computation.
Furthermore, the interplay between quantum entanglement and qubit representation spurs fascinating avenues of inquiry. Entangled qubits exhibit correlations that transcend classical bounds. Exploring how distinct representations interact and give rise to entangled states can elucidate profound questions regarding the nature of reality and information itself. Quantum teleportation—a process that allows the transfer of qubit states across distances—demonstrates the complexities and capabilities afforded by entangled qubit systems.
In conclusion, the physical representations of qubits span a plethora of systems and techniques, from superconducting circuits to trapped ions and beyond. Each representation unveils distinct advantages and limitations, reflecting the multifaceted nature of quantum information processing. As research and development in quantum computing continue to advance, understanding these representations not only enhances theoretical comprehension but also catalyzes practical applications, shaping the future of technology conjoined with the awe-inspiring principles of quantum mechanics.