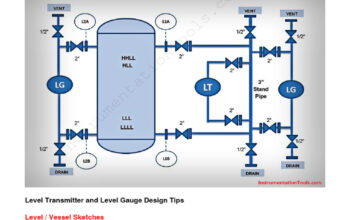
Measurement is a fundamental concept that permeates various scientific disciplines, serving as the cornerstone for empirical inquiry and quantitative analysis. In the realm of science, technology, and engineering, the precise measuring processes of measurement are crucial for ensuring accuracy, reliability, and replicability of results. This article delves into the intricate processes involved in measurement, elucidating the nuances across different measurement types and their implications.
At its core, measurement is the act of assigning numbers to phenomena according to specific rules, which can be categorized into different types: qualitative and quantitative measurements. While qualitative measurements involve the discernment of attributes or characteristics without numerically quantifying them—such as colors, textures, or flavors—quantitative measurements pertain to numerical data that can be expressed in units. This distinction is fundamental, as it shapes the methodologies utilized in various research domains.
Quantitative measurements can be further delineated into continuous and discrete types. Continuous measurements permit infinite subdivisions, enabling the acquisition of values within a range. For instance, the measurement of temperature on a thermodynamic scale is continuous, allowing for decimal representation. On the contrary, discrete measurements consist of distinct values, typically represented in whole numbers. This can be exemplified by counting the number of atoms in a sample, where fractional atoms cannot exist.
When considering the measuring processes of measurement, one must also address the systematic methodologies employed to ensure reliability. Calibration emerges as a critical aspect in this context. Calibration entails the process of configuring an instrument to provide a result for a sample within an acceptable range. This procedure is vital for maintaining the integrity of measurements. For example, in metrology, the practice of calibrating weight scales against a standardized mass guarantees that the measurements are accurate and consistent over time.
Moreover, the concept of measurement uncertainty plays a pivotal role in understanding the quality of data. Measurement uncertainty refers to the doubt that exists about the result of a measurement. It can arise from various sources, including instrumental limitations, environmental conditions, and human error. The propagation of uncertainty must be meticulously calculated, employing statistical methods such as standard deviation and confidence intervals. These methodologies assist researchers in quantifying the reliability of their measurements and ensuring the robustness of their findings.
Another salient facet of measurement processes is the distinction between direct and indirect measurements. Direct measurements involve immediate observation of a quantity, using tools such as rulers, scales, or volume meters. For instance, measuring the height of a liquid in a graduated cylinder exemplifies a direct measurement. In contrast, indirect measurements necessitate calculating a desired quantity using one or more measurable quantities. An instance of this is computing the area of a rectangle from its length and width; the length and width are directly measured, while the area is derived from these direct measurements.
Furthermore, in the modern scientific landscape, the advent of technology has revolutionized measuring processes, introducing precision and efficiency in data acquisition. For instance, digital measurement devices employ advanced algorithms and sensors that yield remarkably precise outputs, minimizing human error. Technologies such as laser measuring devices and digital oscilloscopes exemplify the sophistication of contemporary measurement techniques. Such advancements necessitate a continuous dialogue between traditional measurement methodologies and innovative technological applications, prompting ongoing research in measurement science.
The context of measurement processes also encompasses the application of statistical techniques to ascertain the validity of measurement results. Statistical analysis plays a critical role during the interpretation phase, ensuring that the conclusions drawn from data are statistically significant. Besides verifying hypothesis validity, it assists in identifying correlation coefficients, regression models, and variability within datasets. Proper application of these statistical methodologies can decisively inform experimental design and enhance the overall robustness of scientific investigations.
As we explore the overarching implications of measurement processes, it is evident that ethical considerations are paramount. The responsibility of researchers extends beyond merely gathering data; it includes the integrity of the measurement process itself. Ensuring transparency in methodology, openly discussing measurement uncertainties, and acknowledging limitations are essential to uphold ethical standards in scientific research. Such ethical practices cultivate trust in the scientific community and among the public, reinforcing the credibility of scientific discourse.
In conclusion, the measuring processes of measurement encompass a vast array of practices that are fundamental to scientific inquiry. Through a comprehensive understanding of qualitative and quantitative distinctions, calibration significance, the interplay of direct and indirect measurements, and technological advancements, one can appreciate the complexities involved in achieving reliable measurement outcomes. Coupled with an awareness of statistical applications and ethical ramifications, this knowledge not only enriches scientific endeavors but also fosters a culture of integrity within the empirical community. As the landscape of scientific measurement continues to evolve, the importance of meticulous measuring processes will remain an indelible cornerstone of credible research.